
如图,AB为量角器(半圆O)的直径,等腰直角△BCD的斜边BD交量角器边缘于点G,直角边CD切量角器于读数为60°的点E处(即弧AE的度数为60°),第三边交量角器边缘于点F处.
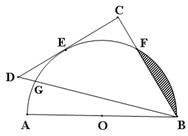
(1)求量角器在点G处的读数α(0°<α<90°);
(2)若AB=10cm,求阴影部分面积.
(1)30° ;(2)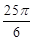 -
-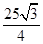
【解析】
试题分析:(1)连接OE,OF,先根据切线的性质可得OE⊥CD,再根据BD为等腰直角△BCD的斜边,可得BC⊥CD,∠D=∠CBD=45°,即可证得OE∥BC,则有∠ABC=∠AOE=60°,即得∠ABG的度数,从而可以求得结果;
(2)先证得△OBF为正三角形,先根据阴影部分的面积等于扇形OBF的面积-三角形OBF的面积,结合扇形的面积公式及三角形的面积公式求解即可.
(1)连接OE,OF

∵CD切半圆O于点E
∴OE⊥CD,
∵BD为等腰直角△BCD的斜边,
∴BC⊥CD,∠D=∠CBD=45°,
∴OE∥BC
∴∠ABC=∠AOE=60°,
∴∠ABG=∠ABC-∠CBD=60°-45°=15°
∴弧AG的度数=2∠ABG=30°,
∴量角器在点G处的读数α=弧AG的度数=30° ;
(2)∵OF=OB=0.5AB=5cm,∠ABC=60°,
∴△OBF为正三角形,∠BOF=60°,
∴S扇形=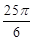 (cm2),S△OBF=
(cm2),S△OBF=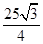
∴S阴影=S扇形-S△OBF=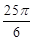 -
-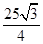
考点:切线的性质,等腰直角三角形的性质,圆周角定理,扇形、三角形的面积公式
点评:本题知识点较多,综合性较强,是中考常见题,熟练掌握圆的相关性质是解题关键.


科目:初中数学 来源: 题型:
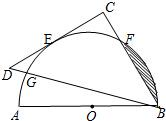 如图,AB为量角器(半圆O)的直径,等腰直角△BCD的斜边BD交量角器边缘于点G,直角边CD切量角器于读数为60°的点E处(即弧AE的度数为60°),第三边交量角器边缘于点F处.
如图,AB为量角器(半圆O)的直径,等腰直角△BCD的斜边BD交量角器边缘于点G,直角边CD切量角器于读数为60°的点E处(即弧AE的度数为60°),第三边交量角器边缘于点F处.查看答案和解析>>
科目:初中数学 来源: 题型:
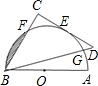 于读数为60°的点E处(即弧AE的度数为60°),第三边交量角器边缘于点F处.
于读数为60°的点E处(即弧AE的度数为60°),第三边交量角器边缘于点F处.查看答案和解析>>
科目:初中数学 来源: 题型:
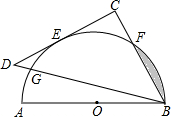 (2013•宁波模拟)如图,AB为量角器(半圆O)的直径,等腰直角△BCD的斜边BD交量角器边缘于点G,直角边CD切量角器于读数为60°的点E处(即弧AE的度数为60°),第三边交量角器边缘于点F处.
(2013•宁波模拟)如图,AB为量角器(半圆O)的直径,等腰直角△BCD的斜边BD交量角器边缘于点G,直角边CD切量角器于读数为60°的点E处(即弧AE的度数为60°),第三边交量角器边缘于点F处.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AB为量角器(半圆O)的直径,△ACD是一块含30°角的直角三角板,且∠CAD=30°,AC、AD分别交半圆O于点E、F.
如图,AB为量角器(半圆O)的直径,△ACD是一块含30°角的直角三角板,且∠CAD=30°,AC、AD分别交半圆O于点E、F. | BE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com