菱形的对角线长分别是6和8,则菱形的周长 ,面积为 .菱形ABCD的周长为20,相邻两内角之比为1:2,则对角线长分别为 .
【答案】
分析:首先根据题意作出图形,然后由菱形的性质,可得AC⊥BD,然后由勾股定理,可求得边长,继而求得菱形的周长,由菱形的面积等于其对角线积的一半,即可求得面积;
由菱形ABCD的周长为20,相邻两内角之比为1:2,即可求得其邻角的度数,然后由含30°角的直角三角形的性质,求得对角线长.
解答:
解:如图,∵在菱形ABCD中,AC=6,BD=8,
∴AC⊥BD,OA=

AC=3,OB=

BD=4,
∴AB=

=5,
∴菱形的周长为:5×4=20;面积为:

×6×8=24;
∵菱形ABCD的相邻两内角之比为1:2,
即∠ABC:∠BAD=1:2,
∵∠ABC+∠BAD=180°,
∴∠ABC=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴AC=AB=20÷4=5;
∴OC=

AC=

,
∵∠OBC=

∠ABC=30°,
∴OB=

=


,
∴BD=5
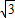
,
∴对角线长分别为,5,5

.
故答案为:20;24;5,5

.
点评:此题考查了菱形的性质、勾股定理以及含30°角的直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

 解:如图,∵在菱形ABCD中,AC=6,BD=8,
解:如图,∵在菱形ABCD中,AC=6,BD=8, AC=3,OB=
AC=3,OB= BD=4,
BD=4, =5,
=5, ×6×8=24;
×6×8=24; AC=
AC= ,
, ∠ABC=30°,
∠ABC=30°, =
=
 ,
,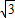 ,
, .
. .
.
