
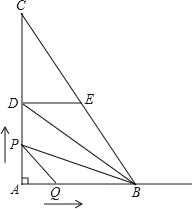
����Ŀ����ͼ����ֱ����ABC�У���A��90����AB��6��AC��8��D��E�ֱ���AC��BC�ߵ��е㣬��P��A�������߶�AD��DE��EB��ÿ��3����λ�����ٶ���B�����˶�����Q�ӵ�A����������AB��ÿ��2����λ�����ٶ������˶�������P���B�غ�ʱֹͣ�˶�����QҲ��ֹ֮ͣ�˶������P��Q�˶�ʱ����t�룬��t��0��
��1����t���� ��ʱ����P�����յ�B��
��2������P�˶�����Dʱ������BPQ�������
��3������BPQ�����ΪS�������Q���߶�AB���˶�ʱ��S��t�ĺ�����ϵʽ��
��4����ֱ��д��PQ��DBʱt��ֵ��
���𰸡���1��4�룻��2��![]() ����3��Q���߶�AB���˶�ʱ��S��t�ĺ�����ϵʽΪS��
����3��Q���߶�AB���˶�ʱ��S��t�ĺ�����ϵʽΪS��![]() ����4��
����4��![]()
��������
��1������֪���ɶ��������BC������D��E�ֱ���AC��BC���е㣬���AD��DE��BE���Ӷ����t��
��2�����������P�˶�����Dʱ����ʱ�䣬�ó�AQ�ij����������BQ�ij����ٸ�����BPQ�����=![]() BQAP���м��㼴�ɣ�
BQAP���м��㼴�ɣ�
��3������֪��t��ʾ��AQ��AP��BQ�����ɡ�A=90����ͨ�������ʽ���S��t�ĺ�����ϵʽ��
��4��ͨ�����裬������������ۼ�����⣮
��1����֪Rt��ABC�У���A��90�㣬AB��6��AC��8��
�ɹ��ɶ����ã�BC��![]() ��
��![]() ��10��
��10��
����D��E�ֱ���AC��BC���е㣬
��AD��4��DE��3��BE��5��
�൱��P�����յ�Bʱ����ʱ��t����4+3+5����3��4���룩��
��t��ֵΪ4�룮
��2������P�˶�����Dʱ������ʱ��Ϊ![]() �룬
�룬
����AQ��![]() ��2��
��2��![]() ��
��
��BQ��6��![]() ��
��![]() ��
��
���BPQ�������![]() BQAP��
BQAP��![]() ��4��
��4��![]() ��
��
��3������ͼ������P��AD�ϣ�������D�㣩��
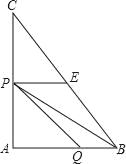
����֪�ã�AQ��2t��AP��3t��
��BQ��AB��AQ��6��2t��
��֪��A��90�㣬
���BPQ�����S��![]() BQAP��
BQAP��![]() ��6��2t��3t����3t2+9t��
��6��2t��3t����3t2+9t��
����Q���߶�AB���˶�ʱ��S��t�ĺ�����ϵʽΪS����3t2+9t��
����ͼ����P��DE��������D��E���ϣ�
����P��PF��AB��F��
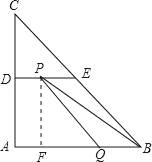
��PF��AD��4��
���BPQ�����S��![]() BQPF��
BQPF��![]() ��6��2t��4��12��4t��
��6��2t��4��12��4t��
���Դ�ʱQ���߶�AB���˶�ʱ��S��t�ĺ�����ϵʽΪS��12��4t��
�۵���P��BE�ϣ�������E�㣩��
����֪�ã�BP��3+4+5��3t��12��3t��
����P��PF��AB��F��
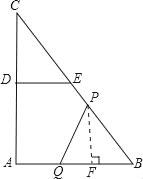
��PF��AC��
���BPF�ס�BCA��
��![]() ��
��
��![]() ��
��
��PF��![]() ��
��
���BPQ�����S��![]() BQPF��
BQPF��![]() ��6��2t��
��6��2t��![]() ��
��![]() ����
����
����Q���߶�AB���˶�ʱ��S��t�ĺ�����ϵʽΪS��![]() ����
����
��4����PQ��DB�����P��Q����DBͬ�࣮�����������
�ٵ���Q��AB�ϣ���P��AD��ʱ��
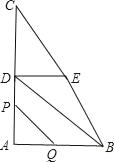
����PQ��DB������
���AQP�ס�ABD��
��![]() ��
��
��![]() ��
��
��ʱ���̵Ľ���t��0�����˽ⲻ�������⣬
��PQ��DB��������
�ڵ�3��t��4ʱ����Q��AB�ӳ����ϣ���P��EB�ϣ�

��ʱPB��12��3t��PE��3t��7��BQ��2t��6��
��PQ��DB����ֱ��PQ��DE��N��
��DE��AB��
���PEN�ס�PBQ��
��EN��BQ��PE��PB��
��EN��![]() ��
��
�֡�NQ��DB��
��EN��ED��EP��EB��
��EN��![]() ��
��
����![]() ��
��![]() ��
��
���t��![]() �������⣮
�������⣮
������������t��![]() ʱ��PQ��DB��
ʱ��PQ��DB��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=12����E�ڱ�BC�ϣ�BE=EC������DCE��DE��������DFE���ӳ�EF����AB�ڵ�G������DG��BF���������н��ۣ��١�DAG�ա�DFG����BG=2AG���ۡ�EBF�ס�DEG����S��BEF=![]() .������ȷ���۵ĸ����ǣ� ��
.������ȷ���۵ĸ����ǣ� ��
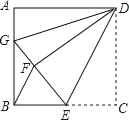
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
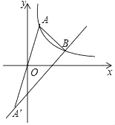
����Ŀ��ƽ��ֱ������ϵxOy�У�������Ϊa�ĵ�A�ڷ���������y1��![]() (x��0)��ͼ���ϣ���A���A���ڵ�O�Գƣ�һ�κ���y2��mx+n��ͼ����A��
(x��0)��ͼ���ϣ���A���A���ڵ�O�Գƣ�һ�κ���y2��mx+n��ͼ����A��
(1)��a��2����B(4��2)�ں���y1��y2��ͼ���ϣ�
���ֱ�����y1��y2�ı���ʽ��
��ֱ��д��ʹy1��y2��0������x�ķ�Χ��
(2)��ͼ���躯��y1��y2��ͼ���ཻ�ڵ�B����B�ĺ�����Ϊ3a����AA��B�����Ϊ16����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣�һ����ϵ���״�����������ABC����BC=120mm����AD=80mm�������ӹ��������������ͼ1��ʹ�����ε�һ����BC�ϣ�������������ֱ���AB��AC�ϣ�

��1����֤����AEF�ס�ABC��
��2�����������������ı߳���
��3����������ӹ��ɾ��������ͼ2����������ε��������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC�У���ABC=90�㣬AB=3��BC=4����Q���߶�AC�ϵ�һ�����㣬����Q��AC�Ĵ��߽��߶�AB����ͼ1�����߶�AB���ӳ��ߣ���ͼ2���ڵ�P��
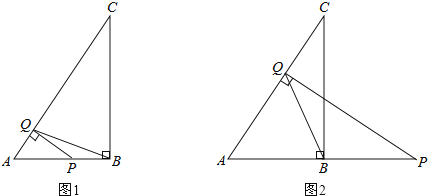
��1������P���߶�AB��ʱ����֤����APQ�ס�ABC��
��2������PQBΪ����������ʱ����AP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ŀ�ĸ���Ĵ�������2018��10��24����ʽͨ����������������������Ŀ纣���ţ���Ӣ������������Ϊ���������ߴ��漣���������������������շ�վʱ�����ѿ��ŵ�4���շ�ͨ��A��B��C��D�п����ѡ������һ��ͨ����
��1��һ���������շ�վʱ��ѡ��Aͨ��ͨ���ĸ������� ����
��2������״ͼ���б������������������շ�վʱ��ѡ��ͬͨ��ͨ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���⽻ͨӵ�£�ij����ƻ���һ����ͨ������ͨ��һ���ֵĽ�����ͼ��ʾ��ͼ�е���AD��ͨ��BCƽ�У�ͨ��ˮƽ����BCΪ8�ף���BCD=135����ͨ��б��CD�ij�Ϊ6�ף�ͨ��б��AB���¶�i=1��![]() ��
��
��1����ͨ��б��AB�ij���
��2��Ϊ�����������ߵ����ʶȣ��⽫���ͼ�е�ͨ��б��CD���¶ȱ仺���ĺ��ͨ��б��DE���½�Ϊ30�������ʱBE�ij���
���𰸾���ȷ��0.1�ף��ο����ݣ�![]() ��1.41��
��1.41��![]() ��2.24��
��2.24��![]() ��2.45��
��2.45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�У�BD�ǶԽ��ߣ���ABC=90�㣬tan��ABD=![]() ��AB=20��BC=10��AD=13�����߶�CD=__��
��AB=20��BC=10��AD=13�����߶�CD=__��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com