Question

15．我市某中学开展爱心捐款活动．团干部小华对九（1）班的捐款情况进行了统计，并把统计的结果制成一个不完整的频数分布直方图的扇形统计图．已知学生捐款最少的是5元，最多的不足25元．
（1）请补全频数分布直方图；
（2）九（1）班学生捐款的中位数所在的组别范围是15-20；
（3）九（1）班学生小明同学捐款22元，班主任拟在捐款最多的20～25元这组同学中随机选取一人代表班级在学校组织的献爱心活动大会上发言，小明同学被选中的概率是0.1．

Answer 1

分析 （1）先求九（1）班的总人数，再分别算出捐款数在20-25之间的人数和捐款数在10-15之间的人数，补全条形图；
（2）先计算出中位数，再找中位数所在的范围；
（3）计算出20-25这个范围的人数，再求概率．

解答 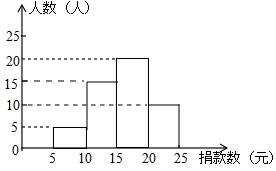解：（1）九（1）班共有：5÷10%=50（人）；
该班捐款20～25元有：50×20%=10（人）；
该班捐款10～15元有：50-5-20-10=15（人）．
（2）按捐款数从小到大排列，第25、26人的捐款数在15-20这组中．
故答案为15-20
（3）小明同学被选中的概率是：$\frac{1}{10}$=0.1．
故答案为0.1．

点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力．利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．用到的知识点为：概率=所求情况数与总情况数之比．部分数目=总体数目乘以相应概率．一组数据按顺序排列后，中间的那两个数的平均数或中间的那个数叫做中位数