
【题目】如图,已知AB是⊙O的直径,BC与⊙O相切于点B,连接OC,交⊙O于点E,弦AD∥OC.
(1)求证:点E是弧BD的中点;(2)求证:CD是⊙O的切线.
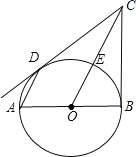
【答案】(1)见解析;(2)见解析
【解析】
(1)连接OD.根据相等的圆心角所对的弧相等,证明∠COD=∠COB后得证;
(2)证明OD⊥CD即可.通过证明△COD≌△COB得∠ODC=∠OBC=90°得证.
证明:(1)连接OD.
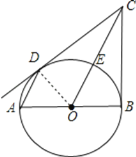
∵AD∥OC,
∴∠ADO=∠COD,∠A=∠COB.
∵OA=OD,
∴∠A=∠ADO.
∴∠COD=∠COB.
∴弧BE=弧DE,即点E是弧BD的中点.
(2)由(1)可知∠COD=∠COB,
在△COD和△COB中,
 ,
,
∴△COD≌△COB,
∴∠CDO=∠CBO.
∵BC与⊙O相切于点B,
∴BC⊥OB,即∠CBO=90°.
∴∠CDO=90°,即DC⊥OD.
∴CD是⊙O的切线.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一圆弧形桥拱的圆心为![]() ,拱桥的水面跨度
,拱桥的水面跨度![]() 米,桥拱到水面的最大高度
米,桥拱到水面的最大高度![]() 为
为![]() 米.求:
米.求:
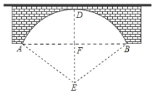
![]() 桥拱的半径;
桥拱的半径;
![]() 现水面上涨后水面跨度为
现水面上涨后水面跨度为![]() 米,求水面上涨的高度为________米.
米,求水面上涨的高度为________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图一张三角形纸片ABC,边AB长为10cm,AB边上的高为15cm,在三角形内从左到右叠放边长为2的正方形小纸片,第一次小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放的正方形的个数是( ).
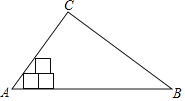
A. 12B. 13C. 14D. 15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=6,将△ABC绕点A逆时针方向旋转60°得到△AB′C′,求线段B′C的长.
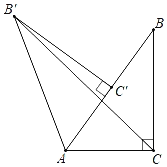
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种商品的进价为每件30元该商品在第x天的售价是y1(单位:元/件),销量是y2(单位:件),且满足关系式![]() ,y2=200﹣2x,设每天销售该商品的利润为w元.
,y2=200﹣2x,设每天销售该商品的利润为w元.
(1)写出w与x的函数关系式;
(2)销售该商品第几天时,当天销售利润最大?最大利润是多少?
(3)该商品销售过程中,共有多少天日销售利润不低于4800元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A、B,与x轴的另一个交点为C,顶点为D.
(1)求抛物线的解析式;
(2)画出抛物线的图象;
(3)在x轴上是否存在点N使△ADN为直角三角形?若存在,求出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com