
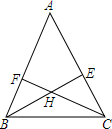
 已知:如图,BE和CF是△ABC的高,H是BE和CF的交点,且HB=HC,∠A=60°,求证:△ABC为等边三角形.
已知:如图,BE和CF是△ABC的高,H是BE和CF的交点,且HB=HC,∠A=60°,求证:△ABC为等边三角形.  状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:解答题
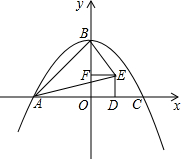 如图,二次函数y=-$\frac{1}{k}$x2+k(k>0)的图象与x轴相交于A、C两点(点A在点C的左侧),与y轴交于点B,点D为线段OC上一点(不与点O、C重合),以OD为边向上作正方形ODEF,连接AE,BE,AB,AB,设点D的横坐标为m.
如图,二次函数y=-$\frac{1}{k}$x2+k(k>0)的图象与x轴相交于A、C两点(点A在点C的左侧),与y轴交于点B,点D为线段OC上一点(不与点O、C重合),以OD为边向上作正方形ODEF,连接AE,BE,AB,AB,设点D的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
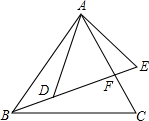 如图,点B、D、E在一条直线上,BE与AC相交于点F,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,若∠EAC=18°,则∠EBC=18°.
如图,点B、D、E在一条直线上,BE与AC相交于点F,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,若∠EAC=18°,则∠EBC=18°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 太阳从西方升起 | B. | 打开电视正在播放《新闻联播》 | ||
| C. | 若a≤0,则|a|=-a | D. | 某运动员投篮时连续3次全中 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com