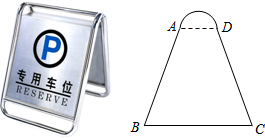
等腰梯形ABCD的上、下底之和为4，两条对角线所夹锐角为60°，则该等腰梯形的高为________．
或
分析：首先根据题意画出图形，然后过点D作DF∥AC，交BC的延长线于点F，易得四边形ACFD是平行四边形，△DBF是等腰三角形，然后分别从若∠AOB=60°与若∠BOC=60°去分析求解即可求得答案．
解答：
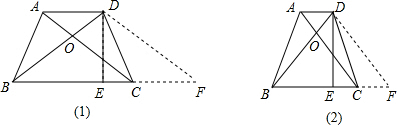
解：过点D作DF∥AC，交BC的延长线于点F，
∵AD∥BC，
∴四边形ACFD是平行四边形，
∴CF=AD，DF=AC，
∴BF=BC+CF=BC+AD=4，
∵等腰梯形ABCD中，BD=AC，
∴BD=DF，
∵DE⊥BC，
∴BE=
BF=2，
如图（1），若∠AOB=60°，
∴∠BDF=∠BOC=120°，
∴∠DBC=30°，
∴DE=BE•tan30°=
；
如图（2），若∠BOC=60°，
则∠BDC=60°，
∴∠DBC=30°，
∴DE=BE•tan60°=2
．
∴该等腰梯形的高为：
或
．
故答案为：
或
．
点评：此题考查了等腰梯形的性质、平行四边形的判定与性质以及等腰三角形的性质．此题难度适中，注意掌握辅助线的作法，注意数形结合思想与分类讨论思想的应用．
