
【题目】已知AP是△ABC的外角平分线,连结PB、PC.
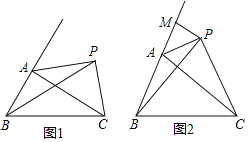
(1)如图1①若BP平分∠ABC,且∠ACB=28°,求∠APB的度数.
②若P与A不重合,请判断AB+AC与PB+PC的大小关系,并证明你的结论.
(2)如图2,若过点P作PM⊥BA,交BA的延长线于M点,且∠BPC=∠BAC,求:![]() 的值.
的值.
【答案】(1)①14°;②PB+PC>AB+AC,证明见解析;(2)![]()
【解析】
(1)根据三角形的角平分线的定义和三角形外角的性质即可得到结论;
(2)在射线AD上取一点H,是的AH=AC,连接PH.则△APH≌△APC,根据三角形的三边关系即可得到结论.
(3)过P作PN⊥AC于N,根据角平分线的性质得到PM=PN,根据全等三角形的性质得到AM=AN,BM=CN,于是得到结论.
解:(1)①∵AP平分∠DAC,PB平分∠ABC,
∴∠DAP=![]() ∠DAC,∠ABP=
∠DAC,∠ABP=![]() ∠ABC,
∠ABC,
∵∠DAC=∠ABC+∠ACB,∠DAP=∠ABP+∠APB,
∴∠APB=∠DAP﹣∠ABP=![]() ∠DAC﹣
∠DAC﹣![]() ∠ABC=
∠ABC=![]() ∠ACB=14°;
∠ACB=14°;
②PB+PC>AB+AC.
理由如下:
如图1﹣1,在射线AD上取一点H,使AH=AC,连接PH.
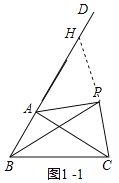
∵AC=AH,∠PAD=∠PAC,AP=AP,
∴△APH≌△APC(SAS),
∴PC=PH,
在△BPH中,PB+PH>BH,
∴PB+PC>AB+AC.
(2)过点P作PN⊥AC于N,
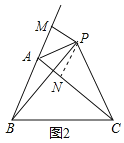
∵AP平分∠MAN,PM⊥BA,
∴PM=PN,
在Rt△APM与Rt△APN中,
![]() ,
,
∴Rt△APM≌Rt△APN(HL),
∴AM=AN,
∵∠BAC=∠BPC,
∴由“8字形”得:∠MBP=∠PCN,
在△PMB与△PNC中,
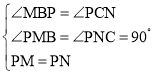 ,
,
∴△PMB≌△PNC(AAS)
∴BM=CN,
∵AM=AN,
∴AC﹣AB=2AM,
∴![]() =
=![]() =
=![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,已知AB∥CD,AD⊥AB,AD=2,AB+CD=4,点E为BC的中点.

(1)求四边形ABCD的面积;
(2)若AE⊥BC,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:在平面直角坐标系中,如果点P的坐标为(m,n),向量![]() 可以用点P的坐标表示为:
可以用点P的坐标表示为:![]() =(m,n).已知
=(m,n).已知![]() =(x1,y1),
=(x1,y1),![]() =(x2,y2),如果x1x2+y1y2=0,那么
=(x2,y2),如果x1x2+y1y2=0,那么![]() 与
与![]() 互相垂直,在下列四组向量中,互相垂直的是( )
互相垂直,在下列四组向量中,互相垂直的是( )
A.![]() =(3,20190),
=(3,20190),![]() =(﹣3﹣1,1)
=(﹣3﹣1,1)
B.![]() =(
=(![]() ﹣1,1),
﹣1,1),![]() =(
=(![]() +1,1)
+1,1)
C.![]() =(
=(![]() ),
),![]() =((﹣
=((﹣![]() )2,8)
)2,8)
D.![]() =(
=(![]() +2,
+2,![]() ),
),![]() =(
=(![]() ﹣2,
﹣2,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:![]() ≈2.449,结果保留整数)
≈2.449,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,∠BAD=80°,C为BD延长线上一点,∠BAC=130°,∠ABD的角平分线与AC交于点E,连接DE.

(1)求证:点E到DA、DC的距离相等;
(2)求∠BED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a=2 002x+2 003,b=2 002x+2 004,c=2 002x+2 005,则多项式a2+b2+c2-ab-bc-ca的值为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300![]() 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),

(1)求围栏的长和宽;
(2)能否围成面积为400 ![]() 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,D在线段AB上,△PCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,△ACP∽△PDB?
(2)当△ACP∽△PDB时,求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人设摊“摸彩”,只见他手持一袋,内装大小、质量完全相同的![]() 个红球、
个红球、![]() 个白球,每次让顾客“免费”从袋中摸出两球,如果两球的颜色相同,顾客得
个白球,每次让顾客“免费”从袋中摸出两球,如果两球的颜色相同,顾客得![]() 元钱,否则顾客付给这人
元钱,否则顾客付给这人![]() 元钱,请你判断一下该活动对顾客________(填“合算”或“不合算”).
元钱,请你判断一下该活动对顾客________(填“合算”或“不合算”).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com