
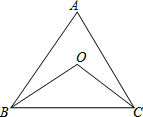
 如图,点O是△ABC的∠ABC、∠ACB的平分线的交点,若∠A为锐角,∠BOC=α°,则α的取值范围为90°<α<135°.
如图,点O是△ABC的∠ABC、∠ACB的平分线的交点,若∠A为锐角,∠BOC=α°,则α的取值范围为90°<α<135°. 分析 根据三角形的内角和定理和角平分线的定义求出∠OBC+∠OCB的度数,再根据三角形的内角和等于180°,即可求出∠BOC=90°+$\frac{1}{2}$∠A,根据A的取值范围得出∠BOC的范围.
解答 解:∵∠A=60°,
∴∠ABC+∠ACB=180°-∠A=180°-60°=120°,
∵BO,CO分别是∠ABC,∠ACB的平分线,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB),
∴∠BOC=180°-(∠OBC+∠OCB)=180°-$\frac{1}{2}$(∠ABC+∠ACB)=180°-$\frac{1}{2}$(180°-∠A)=90+$\frac{1}{2}$∠A,
∵0°<∠A<90°,
∴90°<∠BOC<135°.
故答案为:90°<α<135°
点评 此题考查三角形的内角和定理和角平分线的定义,熟练掌握定理和概念是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,一棵树(AB)的高度为7.5米,下午某一个时刻它在水平地面上形成的树影长(BE)为10米,现在小明想要站这棵树下乘凉,他的身高为1.5米,那么他最多可以离开树干多少米才可以不被阳光晒到?
如图,一棵树(AB)的高度为7.5米,下午某一个时刻它在水平地面上形成的树影长(BE)为10米,现在小明想要站这棵树下乘凉,他的身高为1.5米,那么他最多可以离开树干多少米才可以不被阳光晒到?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2016 | B. | 1 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | -2 | C. | -3 | D. | -$\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
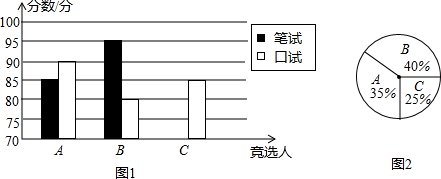
| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 口试 | 80 | 85 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com