
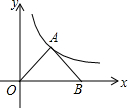
 已知,如图所示,在平面直角坐标系中,Rt△OAB的直角顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,∠AOB=30°,顶点B在x轴上,求此△OAB顶点A的坐标和△OAB面积.
已知,如图所示,在平面直角坐标系中,Rt△OAB的直角顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,∠AOB=30°,顶点B在x轴上,求此△OAB顶点A的坐标和△OAB面积. 分析 作AC⊥OB于C,设OC=x,根据题意得AC=$\frac{\sqrt{3}}{3}$x,则A(x,$\frac{\sqrt{3}}{3}$x),根据k=x•$\frac{\sqrt{3}}{3}$x=4$\sqrt{3}$,进一步求得A的坐标,根据射影定理求得BC,最后根据三角形面积求得即可.
解答 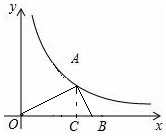 解:作AC⊥OB于C,
解:作AC⊥OB于C,
∵∠AOB=30°,
∴设OC=x,则AC=$\frac{\sqrt{3}}{3}$x,
∴A(x,$\frac{\sqrt{3}}{3}$x),
∵顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,
∴x•$\frac{\sqrt{3}}{3}$x=4$\sqrt{3}$,
∴x=2$\sqrt{3}$,
∴A(2$\sqrt{3}$,2 ),
∴OC=2$\sqrt{3}$,AC=2,
∵在Rt△AOB中,AC2=OC•BC,
∴BC=$\frac{2\sqrt{3}}{3}$,
∴S△AOB=$\frac{1}{2}$×(2$\sqrt{3}$+$\frac{2\sqrt{3}}{3}$)×2=$\frac{8\sqrt{3}}{3}$.
点评 本题考查了反比例函数系数k的几何意义,利用了射影定理,三角形的面积公式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
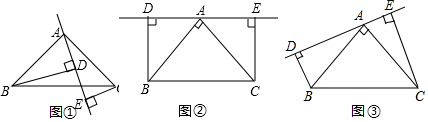
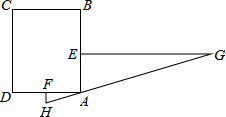 “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB、AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过点A,问FH多少里?
“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB、AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过点A,问FH多少里?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
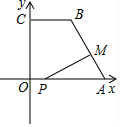 如图,在平面直角坐标系中,已知点A(10,0),B(4,8),C(0,8),连接AB,BC,点P在x轴上,从原点O出发,以每秒1个单位长度的速度向点A运动,同时点M从点A出发,以每秒2个单位长度的速度沿折线A-B-C向点C运动,其中一点到达终点时,另一点也随之停止运动,设P,M两点运动的时间为t秒.
如图,在平面直角坐标系中,已知点A(10,0),B(4,8),C(0,8),连接AB,BC,点P在x轴上,从原点O出发,以每秒1个单位长度的速度向点A运动,同时点M从点A出发,以每秒2个单位长度的速度沿折线A-B-C向点C运动,其中一点到达终点时,另一点也随之停止运动,设P,M两点运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
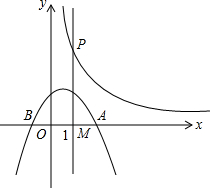 如图,抛物线L:y=-$\frac{1}{2}$(x-t)(x-t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=12.
如图,抛物线L:y=-$\frac{1}{2}$(x-t)(x-t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com