
����Ŀ��ij��˾����![]() �����豸����֪ÿ̨
�����豸����֪ÿ̨![]() ���豸�ijɱ���
���豸�ijɱ���![]() ���豸��1��5������˾��Ͷ��6��Ԫ����
���豸��1��5������˾��Ͷ��6��Ԫ����![]() ���豸��Ͷ��15��Ԫ����
���豸��Ͷ��15��Ԫ����![]() ���豸��������������豸��40̨�������������⣺
���豸��������������豸��40̨�������������⣺
��1��![]() �����豸ÿ̨�ijɱ��ֱ��Ƕ�����Ԫ��
�����豸ÿ̨�ijɱ��ֱ��Ƕ�����Ԫ��
��2����![]() �����豸ÿ̨���ۼ۷ֱ���5000Ԫ��9000Ԫ����˾�������������豸��50̨��������
�����豸ÿ̨���ۼ۷ֱ���5000Ԫ��9000Ԫ����˾�������������豸��50̨��������![]() ���豸��������10̨���ƻ����ۺ����������12��Ԫ�����ʲ�����������������˾���������������������
���豸��������10̨���ƻ����ۺ����������12��Ԫ�����ʲ�����������������˾���������������������
���𰸡���1��![]() ���豸ÿ̨�ijɱ���0.4��Ԫ��
���豸ÿ̨�ijɱ���0.4��Ԫ��![]() ���豸ÿ̨�ijɱ���0.6��Ԫ����2����˾����10̨
���豸ÿ̨�ijɱ���0.6��Ԫ����2����˾����10̨![]() ���豸��40̨
���豸��40̨![]() ���豸ʱ������������������Ϊ130000Ԫ��
���豸ʱ������������������Ϊ130000Ԫ��
��������
��1����A���豸ÿ̨�ijɱ���x��Ԫ��B���豸ÿ̨�ijɱ���1.5x��Ԫ�����ݡ��������ܼۡµ��ۡ���ϡ�Ͷ��Ͷ��1.5��Ԫ����A���豸��3.75��Ԫ����B���豸��������������豸��10̨�������ɵó�����x�ķ�ʽ���̣���֮������ɵó����ۣ�
��2���蹫˾�������ΪWԪ��A���豸����ą����B���豸������50��a��̨���������ۺ����������12��Ԫ��A���豸��������10̨�����ɵó�����a��һԪһ�β���ʽ�飬��֮���ɵó�a��ȡֵ��Χ����������ó�W��a�ĺ�����ϵʽ���ٸ���һ�κ��������ʽ�ɣ�
�⣺��1����![]() ���豸ÿ̨�ijɱ���
���豸ÿ̨�ijɱ���![]() ��Ԫ����
��Ԫ����![]() ���豸ÿ̨�ijɱ���
���豸ÿ̨�ijɱ���![]() ��Ԫ��
��Ԫ��
�������⣬��![]() ��
��
���![]() ��
��
������![]() �Ƿ�ʽ���̵Ľ⣬
�Ƿ�ʽ���̵Ľ⣬
��![]() ��
��
��![]() ���豸ÿ̨�ijɱ���0��4��Ԫ��
���豸ÿ̨�ijɱ���0��4��Ԫ��![]() ���豸ÿ̨�ijɱ���0��6��Ԫ��
���豸ÿ̨�ijɱ���0��6��Ԫ��
��2���蹫˾��õ�����Ϊ![]() Ԫ������
Ԫ������![]() ���豸
���豸![]() ̨��������
̨��������![]() ���豸
���豸![]() ̨��
̨��
���������⣬��![]() ��
��
���![]() ��
��
![]() ��
��![]() ��
��
![]() ����
����![]() ��
��
![]() ��
��
![]() ��
��![]() �����������
�����������
![]() ��
��![]() ʱ��������������������Ϊ
ʱ��������������������Ϊ![]() ��Ԫ����
��Ԫ����
�𣺹�˾����10̨![]() ���豸��40̨
���豸��40̨![]() ���豸ʱ������������������Ϊ130000Ԫ��
���豸ʱ������������������Ϊ130000Ԫ��


 ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д� �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
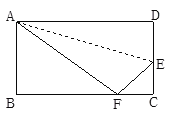
����Ŀ����ͼ��СӨ��һ�ų�����ֽƬABCD������ֽ����֪��ֽƬ��ABΪ8cm��BC��Ϊ10cm����СӨ�۵�ʱ������D����BC���ϵĵ�F��(�ۺ�ΪAE)�����ʱEC=(����)cm
A.4B.![]() C.
C.![]() D.3
D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
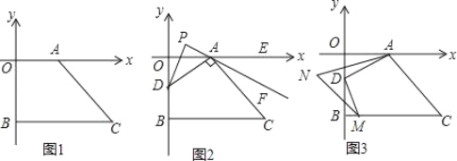
����Ŀ����ͼ1,��ƽ��ֱ������ϵ��,A��a,0����x����������һ��,C�ǵ�������һ��,CB��y��,��y�Ḻ������B��0,b��,��(a-3)2+|b+4|=0,S�ı���AOBC=16��
��1����C�����ꣻ
��2����ͼ2,��DΪ�߶�OB��һ����,��AD��ACʱ,��ODA�Ľ�ƽ�������CAE�Ľ�ƽ���ߵķ����ӳ��߽��ڵ�P,���APD�Ķ�����
��3����ͼ3,��D�����߶�OB���˶�ʱ,��DM��AD��BC��M��,��BMD����DAO��ƽ���߽���N��,��D�����˶�������,��N�Ĵ�С�Ƿ�仯��������,�����ֵ,���仯,˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
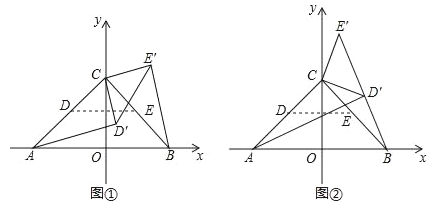
����Ŀ����ƽ��ֱ������ϵ�У��� A����2��0����B��2��0����C��0��2������ D����E�ֱ��� AC��BC���е㣬����CDE�Ƶ�C��ʱ����ת�õ���CD��E��������ת��Ϊ�������� AD����BE����
��1����ͼ������ 0��������90������ AD���CE��ʱ�������Ĵ�С��
��2����ͼ������ 90��������180�������� D�������߶� BE����ʱ���� sin��CBE����ֵ��
��3����ֱ��AD����ֱ��BE���ཻ�ڵ�P�����P�ĺ�����m��ȡֵ��Χ��ֱ��д�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
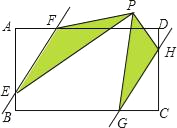
����Ŀ����ͼ���ھ���ABCD�У�AD=6��AB=4����E��G��H��F�ֱ���AB��BC��CD��AD�ϣ���AF=CG=2��BE=DH=1����P��ֱ��EF��GH֮������һ�㣬����PE��PF��PG��PH����ͼ����Ӱ�������PEF����PGH������ͣ����ڣ�������
A. 7 B. 8 C. 12 D. 14
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С�����½�50��ͣ��λ���Խ��С��ͣ���ѵ�����.��֪�½�1������ͣ��λ��1������ͣ��λ��0.5��Ԫ���½�3������ͣ��λ��2������ͣ��λ��1.1��Ԫ.
��1����С���½�1������ͣ��λ��1������ͣ��λ���������Ԫ��
��2������С��Ԥ��Ͷ�ʽ���10��Ԫ��������11��Ԫ�����м��ֽ��췽����
��3����֪ÿ������ͣ��λ�����100Ԫ��ÿ������ͣ��λ�����300Ԫ. �ڣ�2���������£��½�ͣ��λȫ�����.����С������һ������������е�3600Ԫ���ھɳ�λ��ά�ޣ�������������˽��³�λ��ǡ�����꣬��ֱ��д����С��ѡ��������ֽ��췽����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���ACB=60����CEΪ��ABC�Ľ�ƽ���ߣ�AC���ϵĸ�BD��CE���ڵ�ֱ�߽��ڵ�F������ABD:��ACF=2:3�����BEC�Ķ���Ϊ_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣���ͼ����ƽ��ֱ������ϵ�У�OΪԭ�㣬ƽ���ı���ABCD�ı�BC��x���ϣ�D����y���ϣ�C������Ϊ��2��0����BC=6����BCD=60�㣬��E��AB��һ�㣬AE=3EB����P��D��O��C���㣬������![]() ����D��B��C������
����D��B��C������
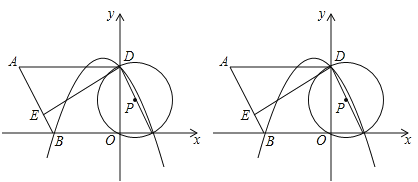
��1���������ߵĽ���ʽ��
��2����֤��ED����P�����ߣ�
��3��������ADE�Ƶ�D��ʱ����ת90�㣬E��Ķ�Ӧ��E�������������![]() ������˵�����ɣ�
������˵�����ɣ�
��4������MΪ�������ߵĶ��㣬ƽ�����Ƿ���ڵ�N��ʹ���Ե�B��D��M��NΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����N�����ꣻ�������ڣ���˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��չ�ˡ��ֻ������С����������������ȡ����ѧ�����С�ʹ���ֻ�Ŀ�ġ��͡�ÿ��ʹ���ֻ���ʱ�䡱���ʾ����飬�����Ƴ�ͼ�١�ͼ�ڲ�������ͳ��ͼ����֪�ʾ������С������ϡ���������40�ˣ�����ͳ��ͼ�С�0��1��ʾÿ��ʹ���ֻ���ʱ�����0Сʱ��С�ڻ����1Сʱ���Դ����ƣ�
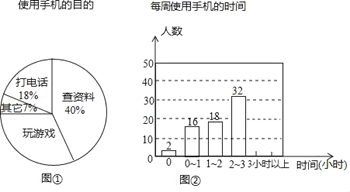
��1�������ʾ�����һ�������˶�����ѧ����
��2����ȫ����ͳ��ͼ��
��3����У����ѧ��1200�ˣ�����ÿ��ʹ���ֻ�������Ϸ���Ƕ�����ѧ����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com