
 如图,直线AC分别交x轴y轴于点A(8,0)、C,抛物线 y=-
如图,直线AC分别交x轴y轴于点A(8,0)、C,抛物线 y=- x2+bx+c(a≠0)经过A,B两点;且OB=OC=
x2+bx+c(a≠0)经过A,B两点;且OB=OC= OA,一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,交抛物线于点P,连接PB、设直线l移动的时间为t秒,
OA,一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,交抛物线于点P,连接PB、设直线l移动的时间为t秒, OA=4,
OA=4, x2+bx+c,
x2+bx+c, ,
, .
. x2+
x2+ x+4;
x+4;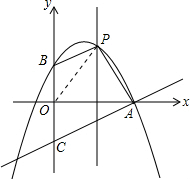 把x=2t代入y=-
把x=2t代入y=- x2+
x2+ x+4,得y=-t2+3t+4,
x+4,得y=-t2+3t+4, ×4×2t+
×4×2t+ ×8×(-t2+3t+4)+
×8×(-t2+3t+4)+ ×4×8
×4×8 (3)①如图,以BP为平行四边形的一边时,BP∥AQ,BP=AQ.
(3)①如图,以BP为平行四边形的一边时,BP∥AQ,BP=AQ. x-4,
x-4, x+m,将B(0,4)代入,
x+m,将B(0,4)代入, x+4.
x+4. ,
,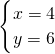 ,
, ②如图,当以BP为平行四边形的对角线时,
②如图,当以BP为平行四边形的对角线时, x-4,
x-4, x-4,解得:y=
x-4,解得:y= x-12,
x-12, x2+
x2+ x+4,
x+4, x2+
x2+ x+4=
x+4= x-12,
x-12, +2,x2=2-2
+2,x2=2-2 (不合题意,舍去).
(不合题意,舍去). +2,
+2, -7).
-7). +2,
+2, -7).
-7). OA=4,确定点B的坐标,然后将A、B两点的坐标代入y=-
OA=4,确定点B的坐标,然后将A、B两点的坐标代入y=- x2+bx+c,即可求出抛物线解析式;
x2+bx+c,即可求出抛物线解析式;

 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
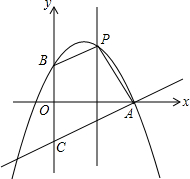 如图,直线AC分别交x轴y轴于点A(8,0)、C,抛物线 y=-
如图,直线AC分别交x轴y轴于点A(8,0)、C,抛物线 y=-| 1 |
| 4 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com