
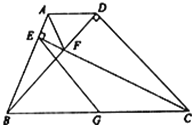
【题目】如图,四边形ABCD中,AD∥BC,∠DCB=45°,CD=2,BD⊥CD.过点C作CE⊥AB于E,交对角线BD于F,点G为BC中点,连接EG、AF.
(1)求EG的长;
(2)求证:CF=AB+AF.
【答案】(1)EG=![]() (2) 见解析
(2) 见解析
【解析】(1)根据BD⊥CD,∠DCB=45°,得到∠DBC=∠DCB,求出BD=CD=2,根据勾股定理求出BC=2![]() ,根据CE⊥BE,点G为BC的中点即可求出EG;
,根据CE⊥BE,点G为BC的中点即可求出EG;
(2)在线段CF上截取CH=BA,连接DH,根据BD⊥CD,BE⊥CD,推出∠EBF=∠DCF,证出△ABD≌△HCD,得到CD=BD,∠ADB=∠HDC,根据AD∥BC,得到∠ADB=∠DBC=45°,推出∠ADB=∠HDB,证出△ADF≌△HDF,即可得到答案.
(1):∵BD⊥CD,∠DCB=45°,
∴∠DBC=45°=∠DCB,∴BD=CD=2,在Rt△BDC中BC=![]() ,
,
∵CE⊥BE,
∠BEC=90°,
∵点G为BC的中点,
∴EG=![]() BC=
BC=![]() .
.
答:EG的长是![]() .
.
(2)证明:在线段CF上截取CH=BA,连接DH,
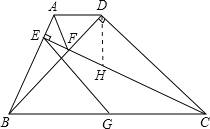
∵BD⊥CD,BE⊥CE,
∴∠EBF+∠EFB=90°,∠DFC+∠DCF=90°,
∵∠EFB=∠DFC,
∴∠EBF=∠DCF,
∵DB=CD,BA=CH,
∴△ABD≌△HCD,
∴AD=DH,∠ADF=∠HDC,
∵AD∥BC,
∴∠ADF=∠DBC=45°,
∴∠HDC=45°,∴∠HDF=∠BDC-∠HDC=45°,
∴∠ADF=∠HDF,
∵AD=HD,DF=DF,
∴△ADF≌△HDF,
∴AF=HF,
∴CF=CH+HF=AB+AF,
∴CF=AB+AF.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
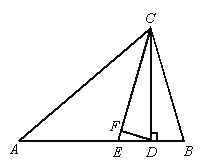
【题目】如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于F,
(1)试说明CD是△CBE的角平分线;
(2)和∠B相等的角是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长江中下游地区特大旱情发生后,全国人民抗旱救灾,众志成城.市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,温州市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
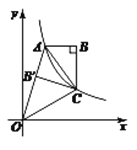
【题目】如图,双曲线![]() (
(![]() >0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与
>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与![]() 轴正半轴的夹角,AB∥
轴正半轴的夹角,AB∥![]() 轴,将△ABC沿AC翻折后得△
轴,将△ABC沿AC翻折后得△![]() ,
,![]() 点落在OA上,则四边形OABC的面积是2,若BC=2,直线
点落在OA上,则四边形OABC的面积是2,若BC=2,直线![]() 与△ABC有交点,求
与△ABC有交点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
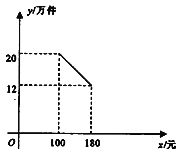
【题目】杰瑞公司成立之初投资1500万元购买新生产线生产新产品,此外,生产每件该产品还需要成本60元.按规定,该产品售价不得低于100元/件且不得超过180元/件,该产品销售量y(万件)与产品售价x(元)之间的函数关系如图所示.
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或者亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,第二年公司重新确定产品售价,能否使两年共盈利达1340万元,若能,求出第二年产品售价;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,0是坐标原点,点A坐标为(2, 0),点B坐标为(0, b) (b>0), 点P是直线AB上位于第二象限内的一个动点,过点P作PC垂直于x轴于点C,记点P关于y轴的对称点为Q.
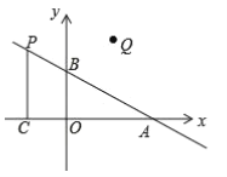
(1)当b=1时:①求直线AB相应的函数表达式:②若![]() ,求点P的坐标:
,求点P的坐标:
(2)设点P的横坐标为a,是否同时存在a、b,使得![]() 是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球运动的一项重要技术.下列图表中的数据分别是甲、乙、内三个运动员十次垫球测试的成绩,规则为每次测试连续垫球10个,每垫球到位1个记1分.
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
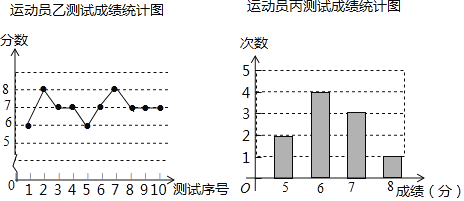
(1)写出运动员甲测试成绩的众数和中位数;
(2)试从平均数和方差两个角度综合分析,若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、s丙2=0.81)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,
,![]() 为原点,且
为原点,且![]() 、
、![]() 满足:
满足:![]() .试解答下列问题:
.试解答下列问题:
(1)求数轴上线段![]() 的长度;
的长度;
(2)若点![]() 以每秒2个单位长度的速度沿数轴向右运动,则经过
以每秒2个单位长度的速度沿数轴向右运动,则经过![]() 秒后点
秒后点![]() 表示的数为 ;(用含
表示的数为 ;(用含![]() 的代数式表示)
的代数式表示)
(3)若点![]() ,
,![]() 都以每秒2个单位长度的速度沿数轴向右运动,而点
都以每秒2个单位长度的速度沿数轴向右运动,而点![]() 不动,经过
不动,经过![]() 秒后其中一个点是一条线段的中点,求此时
秒后其中一个点是一条线段的中点,求此时![]() 的值.
的值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com