
【题目】如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.
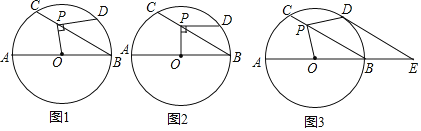
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当![]() 时,延长AB至点E,使BE=
时,延长AB至点E,使BE=![]() AB,连接DE.
AB,连接DE.
①求证:DE是⊙O的切线;
②求PC的长.
【答案】(1)2![]() ;(2)①见解析;②CP的长为:3
;(2)①见解析;②CP的长为:3![]() ﹣3或3
﹣3或3![]() +3.
+3.
【解析】
(1)根据题意首先得出半径长,再利用锐角三角函数关系得出OP,PD的长;
(2)①首先得出△OBD是等边三角形,进而得出∠ODE=∠OFB=90°,求出答案即可;
②首先求出CF的长,进而利用直角三角形的性质得出PF的长,进而得出答案.
解:(1)如图2,连接OD,
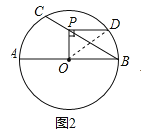
∵OP⊥PD,PD∥AB,
∴∠POB=90°,
∵⊙O的直径AB=12,
∴OB=OD=6,
在Rt△POB中,∠ABC=30°,
∴OP=OBtan30°=6×![]() =2
=2![]() ,
,
在Rt△POD中,
PD=![]() =
=![]() =2
=2![]() ;
;
(2)①证明:如图3,连接OD,交CB于点F,连接BD,
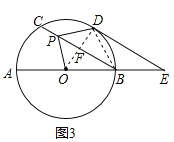
∵![]() ,
,
∴∠DBC=∠ABC=30°,
∴∠ABD=60°,
∵OB=OD,
∴△OBD是等边三角形,
∴OD⊥FB,
∵BE=![]() AB,
AB,
∴OB=BE,
∴BF∥ED,
∴∠ODE=∠OFB=90°,
∴DE是⊙O的切线;
②由①知,OD⊥BC,
∴CF=FB=OBcos30°=6×![]() =3
=3![]() ,
,
在Rt△POD中,OF=DF,
∴PF=![]() DO=3(直角三角形斜边上的中线,等于斜边的一半),
DO=3(直角三角形斜边上的中线,等于斜边的一半),
∴CP=CF﹣PF=3![]() ﹣3,
﹣3,
当点P在点B与点F之间时,同理可得:
![]() +3,
+3,
综上所述:CP的长为:3![]() ﹣3或3
﹣3或3![]() +3.
+3.


科目:初中数学 来源: 题型:
【题目】已知,抛物线![]() 经过点
经过点![]() ,且满足9a+3b+c<0,以下结论:①a+b<0;②4a+c<0;③对于任何x,都有
,且满足9a+3b+c<0,以下结论:①a+b<0;②4a+c<0;③对于任何x,都有![]() ;④
;④![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②③B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个.若从中任意摸出一个球,这个球是白球的概率为0.5.
(1)求口袋中红球的个数.
(2)从袋中任意摸出一球,放回摇匀后,再摸出一球,则两次都摸到白球的概率是多少?请你用列表或画树状图的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①为折叠椅,图②是折叠椅撑开后的侧面示意图,其中椅腿AB和CD的长度相等,O是它们的中点.为使折叠椅既舒适又牢固,厂家将撑开后的折叠椅高度设计为32 cm,∠DOB=100°,那么椅腿AB的长应设计为(结果精确到0.1 cm,参考数据:sin50°=cos40°≈0.77,sin40°=cos50°≈0.64,tan40°≈0.84,tan50°≈1.19)( )

A. 38.1 cm B. 49.8 cm C. 41.6 cm D. 45.3 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
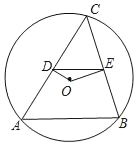
【题目】如图,在圆O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA、CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是点D、E.
(1)求线段DE的长;
(2)点O到AB的距离为3,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
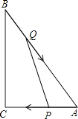
【题目】.如图,在RT△ABC中,∠C=90°,BC=8,AC=6,动点Q从B点开始在线段BA上以每秒2个单位长度的速度向点A移动,同时点P从A点开始在线段AC上以每秒1个单位长度的速度向点C移动.当一点停止运动,另一点也随之停止运动.设点Q,P移动的时间为t秒.当t=____________ 秒时△APQ与△ABC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某空调生产厂的装配车间计划在一段时期内组装9000台空调,设每天组装的空调数量为y(台/天),组装的时间为x(天).
(1)直接写出y与x之间的函数关系式;
(2)原计划用60天完成这一任务,但由于气温提前升高,厂家决定这批空调至少要提前10天完成,那么装配车间每天至少要组装多少台空调?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC⊥BD垂足为点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接NF.
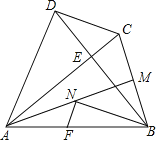
(1)判断线段MN与线段BM的位置关系与数量关系,说明理由;
(2)如果CD=5,求NF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com