
���� ��1������������߶������꣬����OP=OQ�������m������⣮
��2�����÷���������ֱ��DE�������ߵĽ������꣬���������S1-S2���ٸ���m��ȡֵ��Χȷ�����С��
��� �⣺��1����ͼ1�У�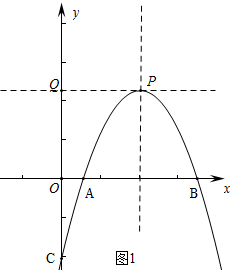
��y=-x2+2mx-m2+2=-��x-m��2+2��
�ඥ��P��m��2����OQ=2��
��OP=OQ��
��m=2��
�������߽���ʽΪy=-x2+4x-2��
��y=0����-x2+4x-2=0��
��x=2��$\sqrt{2}$��
���A���꣨2-$\sqrt{2}$��0����
��2����ͼ2�У��������E��0��m������D��m��0����
��ֱ��ED����ʽΪy=-x+m��
��$\left\{\begin{array}{l}{y=-x+m}\\{y=-{x}^{2}+2mx-{m}^{2}+2}\end{array}\right.$���$\left\{\begin{array}{l}{x=m+2}\\{y=-2}\end{array}\right.$��$\left\{\begin{array}{l}{x=m-1}\\{y=1}\end{array}\right.$��
���M��m+2��-2������N��m-1��1����
��S1=$\frac{1}{2}$��m+m2-2��•��m-1��=$\frac{1}{2}$��m-1��2��m+2����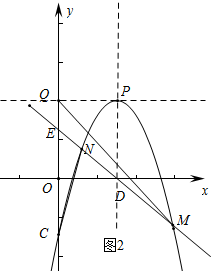
S2=$\frac{1}{2}$��2-m����m+2����
��S1-S2=$\frac{1}{2}$��m+2����m2-m-1����
�ߵ�E���߶�OQ�ϣ���0��m��2��
��������������y�ύ�ڵ�C����x�����������A��B���������ᣬ�������£�
��c��0����-m2+2��0��
��0��m��2��
��$\sqrt{2}$��m��2
�൱$\sqrt{2}$��m��$\frac{1+\sqrt{5}}{2}$ʱ��S1-S2��0����S1��S2��
��m=$\frac{1+\sqrt{5}}{2}$ʱ��S1=S2��
��$\frac{1+\sqrt{5}}{2}$��m��2ʱ��S1-S2��0����S1��S2��
���� ���⿼����κ�����x��Ľ��㡢�䷽��ȷ�����������֪ʶ������Ĺؼ���ѧ�����ò���������⣬ѧ�����ö��κ��������ʱȽ�S1��S2�Ĵ�С����Ŀ�Ƚ��ѣ����п�ѹ���⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢� | C�� | �٢ڢ� | D�� | �٢ڢۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
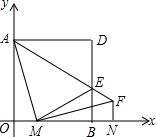 ��ͼ�У�������AOBD�ı�AO��BO���������ϣ����������Ϊ16����M��O����ÿ��1����λ���ȵ��ٶ���x���������˶�����M����B��ʱ���˶�ֹͣ������AM����M��AM��MF��������AM=MF������AF��BD��E�㣬��F��FN��x����N������ME�����M�˶�ʱ��Ϊt��s����
��ͼ�У�������AOBD�ı�AO��BO���������ϣ����������Ϊ16����M��O����ÿ��1����λ���ȵ��ٶ���x���������˶�����M����B��ʱ���˶�ֹͣ������AM����M��AM��MF��������AM=MF������AF��BD��E�㣬��F��FN��x����N������ME�����M�˶�ʱ��Ϊt��s�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3 | B�� | 3 | C�� | $\frac{1}{3}$ | D�� | -$\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
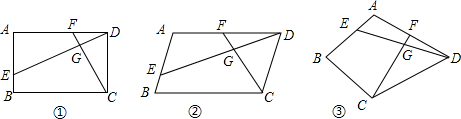 ��֪�ı���ABCD�У�E��F�ֱ���AB��AD���ϵĵ㣬DE��CF���ڵ�G��
��֪�ı���ABCD�У�E��F�ֱ���AB��AD���ϵĵ㣬DE��CF���ڵ�G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | b��a��c | C�� | b��c��a | D�� | c��b��a |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com