
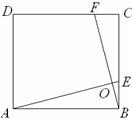
(1) 如图,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.
求证:BE=CF.
(2) 如图,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°, EF=4.求GH的长.

(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,
∠FOH=90°,EF=4. 直接写出下列两题的答案:
①如图1,矩形ABCD由2个全等的正方形组成,求GH的长;
②如图2,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).

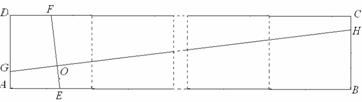
图1 图2
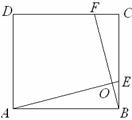
(1) 证明:如图,∵ 四边形ABCD为正方形,
∴ AB=BC,∠ABC=∠BCD=90°,
∴ ∠EAB+∠AEB=90°.
∵ ∠EOB=∠AOF=90°,
∴ ∠FBC+∠AEB=90°,∴ ∠EAB=∠FBC,
∴ △ABE≌△BCF , ∴ BE=CF.
 |
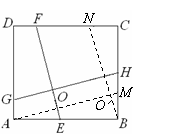
(2) 解:如图,过点A作AM//GH交BC于M,过点B作BN//EF交CD于N,AM与BN交于点O/,则四边形AMHG和四边形BNFE均为平行四边形,
∴ EF=BN,GH=AM,
∵ ∠FOH=90°, AM//GH,EF//BN, ∴ ∠NO/A=90°,
故由(1)得, △ABM≌△BCN, ∴ AM=BN,
∴ GH=EF=4.
 |
3) ① 8.② 4n.


科目:初中数学 来源: 题型:
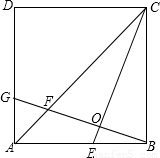
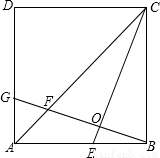
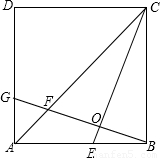
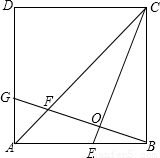
 24、如图,在正方ABCD中,E是AB边上任一点,BG⊥CE,垂足为O,交AC于点F,交AD于点G.
24、如图,在正方ABCD中,E是AB边上任一点,BG⊥CE,垂足为O,交AC于点F,交AD于点G.查看答案和解析>>
科目:初中数学 来源:2013年河南省郑州市荥阳四中中考数学模拟试卷(三)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2012年海南省中考数学模拟试卷(一)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2009年海南省琼海市中考数学模拟试卷(一)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2011年中考复习专项训练《全等三角形》(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com