
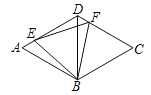
【题目】如图所示,△ABD和△BCD都是等边三角形,E、F分别是边AD、CD上的点,且DE=CF,连接BE、EF、FB.
求证:(1)△ABE≌△DBF;
(2)△BEF是等边三角形.
科目:初中数学 来源: 题型:
【题目】每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如下尚不完整的统计图.
治理杨絮一一您选哪一项?(单选)
A.减少杨树新增面积,控制杨树每年的栽种量
B.调整树种结构,逐渐更换现有杨树
C.选育无絮杨品种,并推广种植
D.对雌性杨树注射生物干扰素,避免产生飞絮
E.其他
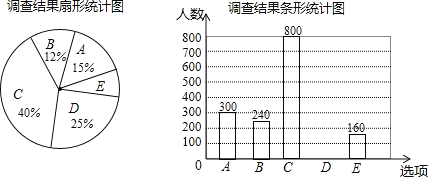
根据以上统计图,解答下列问题:
(1)本次接受调查的市民共有 人;
(2)扇形统计图中,扇形E的圆心角度数是 ;
(3)请补全条形统计图;
(4)若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
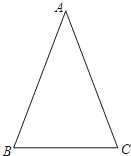
【题目】学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=![]() .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)求sad60°的值;
(2)对于0°<A<180°,求∠A的正对值sadA的取值范围.
(3)已知sinα=![]() ,其中α为锐角,试求sadα的值.
,其中α为锐角,试求sadα的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB和DE是直立在地面上的两根立柱,AB=5 m,某一时刻AB在阳光下的投影BC=2 m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影长时,同时测量出DE在阳光下的投影长为5 m,请你计算DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() ,
,![]() ,
,![]() 与
与![]() 互补,以点
互补,以点![]() 为顶点作一个角,角的两边分别交线段
为顶点作一个角,角的两边分别交线段![]() ,
,![]() 于点
于点![]() ,
,![]() ,且
,且![]() ,连接
,连接![]() ,试探究:线段
,试探究:线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
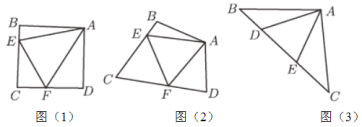
(1)如图(1),当![]() 时,
时,![]() ,
,![]() ,
,![]() 之间的数量关系为___________.
之间的数量关系为___________.
(2)在图(2)的条件下(即不存在![]() ),线段
),线段![]() ,
,![]() ,
,![]() 之间的数量关系是否仍然成立?若成立,请完成证明;若不成立,请说明理由.
之间的数量关系是否仍然成立?若成立,请完成证明;若不成立,请说明理由.
(3)如图(3),在腰长为![]() 的等腰直角三角形
的等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 均在边
均在边![]() 上,且
上,且![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图![]() ,
,![]() ,那么
,那么![]() 成立吗?为什么?下面是小丽同学进行的推理,请你将小丽同学的推理过程补充完整.
成立吗?为什么?下面是小丽同学进行的推理,请你将小丽同学的推理过程补充完整.
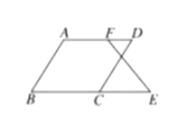
解:成立,理由如下:
![]() (已知)
(已知)
![]() ① (同旁内角互补,两条直线平行)
① (同旁内角互补,两条直线平行)
![]() (② )
(② )
又![]()
![]() (已知),
(已知),![]() (等量代换)
(等量代换)
![]() (③ )
(③ )
![]() (④ ).
(④ ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为![]() ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
(1)求DE的长;
(2)过点EF作EF⊥CE,交AB于点F,求BF的长;
(3)过点E作EG⊥CE,交CD于点G,求DG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com