
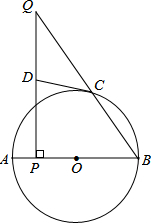
 如图,AB是⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.
如图,AB是⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.分析 (1)连结OC,由OC=OB得∠2=∠B,DQ=DC得∠1=∠Q,根据QP⊥PB得到∠Q+∠B=90°,则∠1+∠2=90°,再利用平角的定义得到∠DCO=90°,然后根据切线的判定定理得到CD为⊙O的切线;
(2)连结AC,由AB为⊙O的直径得∠ACB=90°,根据余弦的定义得cosB=$\frac{BC}{AB}$=$\frac{BC}{AP+BP}$=$\frac{3}{5}$,可计算出BC=$\frac{21}{5}$,在Rt△BPQ中,利用余弦的定义得cosB=$\frac{PB}{BQ}$=$\frac{3}{5}$,可计算出BQ=10,然后利用QC=BQ-BC进行计算即可.
解答 解:(1)CD与⊙O相切.理由如下:
连结OC,如图,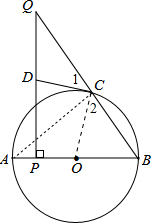
∵OC=OB,
∴∠2=∠B,
∵DQ=DC,
∴∠1=∠Q,
∵QP⊥PB,
∴∠BPQ=90°,
∴∠Q+∠B=90°,
∴∠1+∠2=90°,
∴∠DCO=180°-∠1-∠2=90°,
∴OC⊥CD,
而OC为⊙O的半径,
∴CD为⊙O的切线;
(2)连接AC,如图,
∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,cosB=$\frac{BC}{AB}$=$\frac{BC}{AP+BP}$=$\frac{3}{5}$,
而BP=6,AP=1,
∴BC=$\frac{21}{5}$,
在Rt△BPQ中,cosB=$\frac{PB}{BQ}$=$\frac{3}{5}$,
∴BQ=$\frac{6}{\frac{3}{5}}$=10,
∴QC=BQ-BC=10-$\frac{21}{5}$=$\frac{29}{5}$.
点评 本题考查了切线的判定,圆周角定理的推论,解直角三角形,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是$\frac{3}{10}$ | |
| B. | 随机抛掷一枚均匀的硬币,落地后反面一定朝上 | |
| C. | 某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖 | |
| D. | 在一次课堂进行的抛硬币试验中,同学们估计硬币落地后正面朝上的概率为0.51 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
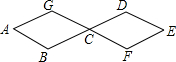 蜜蜂采蜜时,如果蜜源很远它就会跳起“8字舞”,告诉同伴蜜源的方向.如图所示,两个全等菱形的边长为1厘米,一只蜜蜂由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,飞行2015厘米后停下,则这只蜜蜂停在G点.
蜜蜂采蜜时,如果蜜源很远它就会跳起“8字舞”,告诉同伴蜜源的方向.如图所示,两个全等菱形的边长为1厘米,一只蜜蜂由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,飞行2015厘米后停下,则这只蜜蜂停在G点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com