
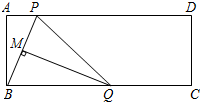
 如图,在矩形ABCD中,点P是边AD上的动点,连结BP,线段BP的垂直平分线交边BC于点Q,垂足为点M,连结QP.已知AD=13,AB=5,设AP=x,BQ=y.
如图,在矩形ABCD中,点P是边AD上的动点,连结BP,线段BP的垂直平分线交边BC于点Q,垂足为点M,连结QP.已知AD=13,AB=5,设AP=x,BQ=y.分析 (1)先证明△ABP∽△MQB,得出对应边成比例$\frac{AP}{MB}=\frac{BP}{QB}$,即可得出结果;
(2)根据题意得⊙P与⊙Q外切时,圆心距PQ=AP+CQ,得出y=x+(13-y),得出y═$\frac{x+13}{2}$,再与(1)中关系式结合,即可得出x的值.
解答 解:(1)∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠APB=∠QBM,BP=$\sqrt{{x}^{2}+25}$,
∵线段BP的垂直平分线交边BC于点Q,
∴∠BMQ=90°,MB=$\frac{\sqrt{{x}^{2}+25}}{2}$,
∴△ABP∽△MQB,
∴$\frac{AP}{MB}=\frac{BP}{QB}$,即$\frac{x}{\frac{\sqrt{{x}^{2}+25}}{2}}=\frac{\sqrt{{x}^{2}+25}}{y}$,
∴$y=\frac{{25+{x^2}}}{2x}$;
(2)∵⊙P与⊙Q外切,圆心距PQ=AP+CQ=x+(13-y),
∵QM是BP的垂直平分线,
∴BQ=PQ=y,
∴y=x+(13-y),
∴y=$\frac{x+13}{2}$,
$\frac{25+{x}^{2}}{2x}$代入(1)得:$\frac{x+13}{2}=\frac{{x}^{2}+25}{2x}$,
解得:x=$\frac{25}{13}$,
经检验,$\frac{25}{13}$是分式方程的解且符合题意.
∴当以AP长为半径的⊙P和以QC长为半径的⊙Q外切时,x的值是$\frac{25}{13}$.
点评 本题考查了相切两圆的性质、矩形的性质、相似三角形的判定与性质以及分式方程的解法;证明三角形相似和由相切两圆的性质得出关系式是解决问题的关键.


科目:初中数学 来源: 题型:填空题
 如图:已知正方形ABCD,动点M、N分别在DC、BC上,且满足∠MAN=45°,△CMN的周长为2,则△CMN面积的最大值是3-2$\sqrt{2}$.
如图:已知正方形ABCD,动点M、N分别在DC、BC上,且满足∠MAN=45°,△CMN的周长为2,则△CMN面积的最大值是3-2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种板材(m2/套) | 乙种板材(m2/套) | 获利(元/套) | |
| A款 | 3 | 7 | 600 |
| B款 | 5 | 3 | 400 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一个锥体的三视图.
如图是一个锥体的三视图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=3cm,⊙O是以BC为直径的圆,如果⊙O与⊙S相内切,那么⊙A的半径为$\sqrt{13}+2$cm.
如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=3cm,⊙O是以BC为直径的圆,如果⊙O与⊙S相内切,那么⊙A的半径为$\sqrt{13}+2$cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com