
����Ŀ����ͼ1��ʾ����������ABCD��������CGEF�У���B��C��G��ͬһ��ֱ���ϣ�M���߶�AE���е㣬DM���ӳ��߽�EF�ڵ�N������FM����֤��DM=FM��DM��FM������д֤�����̣�
��1����ͼ2������B��C��F��ͬһ��ֱ���ϣ�DM���ӳ��߽�EG�ڵ�N�������������䣬��̽���߶�DM��FM�������Ĺ�ϵ����д�����룬������֤����
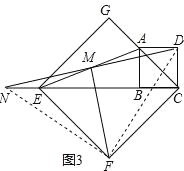
��2����ͼ3������E��B��C��ͬһ��ֱ���ϣ�DM���ӳ��߽�CE���ӳ����ڵ�N�������������䣬̽���߶�DM��FM�������Ĺ�ϵ����ֱ��д�����룮

���𰸡���1��DM��FM��DM=FM��֤����������
��2��DM��FM��DM=FM��
��������
�����������1������DF��NF�����ı���ABCD��CGEF�������Σ��õ�AD��BC��BC��GE�����ǵõ�AD��GE����á�DAM=��NEM��֤�á�MAD�ա�MEN���ó�DM=MN��AD=EN���Ƴ���MAD�ա�MEN��֤����DFN�ǵ���ֱ�������Σ����ɵõ����ۣ�
��2������DF��NF�����ı���ABCD�������Σ��õ�AD��BC���ɵ�E��B��C��ͬһ��ֱ���ϣ����ǵõ�AD��CN����á�DAM=��NEM��֤�á�MAD�ա�MEN���ó�DM=MN��AD=EN���Ƴ���MAD�ա�MEN��֤����DFN�ǵ���ֱ�������Σ����ǽ��۵õ���
�����������1����ͼ2��DM=FM��DM��FM��
֤��������DF��NF��
���ı���ABCD��CGEF�������Σ�
��AD��BC��BC��GE��
��AD��GE��
���DAM=��NEM��
��M��AE���е㣬
��AM=EM��
�ڡ�MAD���MEN�У�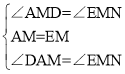 �����MAD�ա�MEN����DM=MN��AD=EN��
�����MAD�ա�MEN����DM=MN��AD=EN��
��AD=CD����CD=NE����CF=EF����DCF=��DCB=90�㣬
�ڡ�DCF���NEF�У�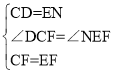 �����MAD�ա�MEN����DF=NF����CFD=��EFN��
�����MAD�ա�MEN����DF=NF����CFD=��EFN��
�ߡ�EFN+��NFC=90�㣬���DFC+��CFN=90�㣬���DFN=90�㣬
��DM��FM��DM=FM
��2�����룺DM��FM��DM=FM��
֤�����£���ͼ3������DF��NF������DF��NF��
���ı���ABCD�������Σ���AD��BC���ߵ�E��B��C��ͬһ��ֱ���ϣ�
��AD��CN�����ADN=��MNE��
�ڡ�MAD���MEN�У�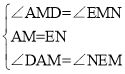 ��
��
���MAD�ա�MEN����DM=MN��AD=EN����AD=CD����CD=NE����CF=EF���ߡ�DCF=90��+45��=135�㣬��NEF=180�㩁45��=135�㣬���DCF=��NEF��
�ڡ�DCF���NEF�У�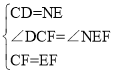 �����MAD�ա�MEN����DF=NF����CFD=��EFN��
�����MAD�ա�MEN����DF=NF����CFD=��EFN��
�ߡ�CFD+��EFD=90�㣬���NFE+��EFD=90�㣬���DFN=90�㣬
��DM��FM��DM=FM��



 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c�ֱ�����ABC�����ߣ���m>0ʱ������x��һԪ���η���c(x2��m)��b(x2��m)��2![]() ax��0��������ȵ�ʵ���������ж���ABC����״����˵�����ɣ�
ax��0��������ȵ�ʵ���������ж���ABC����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧϰ�����ó߹���һ���ǵ�ƽ���ߺ����е�С�Ϸ��֣�ֻ��һ�ѿ̶ȳ�Ҳ��������һ���ǵ�ƽ���ߣ�������������(��ͼ)��
(1)�ֱ��ڡ�AOB������OA��OB�ϸ�ȡһ��C��D��ʹ��OC��OD.
(2)����CD��������CD�ij��ȣ�ȡCD���е�E.
(3)��O��E����������OE����OE���ǡ�AOB��ƽ���ߣ�
����˵��С�������������ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣮
(1)��֪��A(3��1)������OA��ƽ���߶�OA��ʹ��O���ڵ�B.���A���ڵ�C��������̽����
̽��һ������B������Ϊ(1��2)������ͼ��������ƽ�ƺ��ͼ�Σ����C��������______������AC��BO�����ж�O��A��C��B�ĵ㹹�ɵ�ͼ�ε���״����˵�����ɣ�
̽����������B������Ϊ(6��2)����ͼ�ڣ��ж�O��A��B��C�ĵ㹹�ɵ�ͼ�ε���״��
(2)ͨ�������̽������ֱ�ӻش��������⣺
������֪����A��a��b����B��c��d����C��a+c��b+d��(��A��B��C������ԭ��O�غ�)��˳�����ӵ�O��A��C��B�����ж�����ͼ�ε���״��
���ڢٵ������£��������ͼ�������λ��������Σ���ѡ��һ�������д��a��b��c��dӦ����Ĺ�ϵʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���µ����㡰*�������ҹ涨��a*b��a2��2b����3��*����1����_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�ı߳���4����P��AD�ߵ��е㣬��E�������α��ϵ�һ�㣬����PBE�ǵ��������Σ�������Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ������ε��ڽǺ�����Ǻ͵�5������ô�������εı����ǣ�������
A. 10B. 11C. 12D. 13
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ������ʦ����һ������㣺1+21+22+23+24+25+26+27+28+29 �� ��ʦ�ڽ���Ѳ����һȦ������ͬѧ�Ƕ��������������Ǹ����𰸣� �⣺��s=1+21+22+23+24+25+26+27+28+29��
��2s=2+22+23+24+25+26+27+28+29+210��
�ک��ٵ�s=210��1
�������Ϸ�������㣺
��1��1+2+22+23+��+22015��д�����̣�������ݱ�ʾ��
��2��1+3+32+33+��+32015=��������ݱ�ʾ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com