
| A. | a2•a5=a10 | B. | (π-3.14)0=0 | C. | ($\frac{1}{2}$)-2=$\frac{1}{4}$ | D. | $\sqrt{45}$-2$\sqrt{5}$=$\sqrt{5}$ |
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
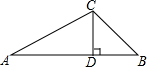 南沙群岛是我国股友领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至A处时,该岛位于正东方向的B处,为了防止某国海巡警干扰,就请求我国C处的渔监船前往B处护航,测得C与AB的距离CD为20海里,已知A位于C处的南偏西60°方向上,B位于C的南偏东45°的方向上,求A、B之间的距离.($\sqrt{3}$≈1.7,结果精确到1海里)
南沙群岛是我国股友领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至A处时,该岛位于正东方向的B处,为了防止某国海巡警干扰,就请求我国C处的渔监船前往B处护航,测得C与AB的距离CD为20海里,已知A位于C处的南偏西60°方向上,B位于C的南偏东45°的方向上,求A、B之间的距离.($\sqrt{3}$≈1.7,结果精确到1海里)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 目的地 | 运费/(元/t) | |
| 甲仓库 | 乙仓库 | |
| A地 | 140 | 200 |
| B地 | 100 | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
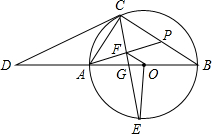 如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,CE交AB于点G,过点A作AF⊥CE于点F,延长AF交BC于点P.
如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,CE交AB于点G,过点A作AF⊥CE于点F,延长AF交BC于点P.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 筹款金额(元) | 10 | 15 | 20 |
| 人数 | 10 | 17 | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com