
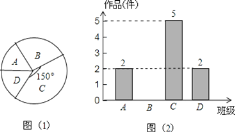
����Ŀ������ij��ѧ�������ڼ䣬��ȫУѧ�������黭��Ʒ![]() ���꼶��������ʦ��ȫ�꼶14�����������ȡ��4���࣬������������Ʒ�����������˷���ͳ�ƣ�����������������������ͳ��ͼ��
���꼶��������ʦ��ȫ�꼶14�����������ȡ��4���࣬������������Ʒ�����������˷���ͳ�ƣ�����������������������ͳ��ͼ��
![]() ����ʦ�������4������������Ʒ�� ��������B����������Ʒ �������ͼ2����������
����ʦ�������4������������Ʒ�� ��������B����������Ʒ �������ͼ2����������
![]() ����ʦ��������ĸ���ƽ��ÿ����������Ʒ���ټ��������ȫ�꼶����������Ʒ���ټ���
����ʦ��������ĸ���ƽ��ÿ����������Ʒ���ټ��������ȫ�꼶����������Ʒ���ټ���
![]() ���ȫ�꼶��չ��Ʒ����5�����һ�Ƚ���������3��������������2��������Ů��
���ȫ�꼶��չ��Ʒ����5�����һ�Ƚ���������3��������������2��������Ů��![]() ����Ҫ�����г�����ȥ�μ�ѧУ�ܽ������̸�ᣬ��ǡ�ó���һ��һŮ�ĸ���
����Ҫ�����г�����ȥ�μ�ѧУ�ܽ������̸�ᣬ��ǡ�ó���һ��һŮ�ĸ���![]() (Ҫ��д������״ͼ���б���������)
(Ҫ��д������״ͼ���б���������)
���𰸡���1��12��3������ͼ�����
��2��4����ƽ����Ʒ��Ϊ��![]() ������������ȫ�꼶����������Ʒ��
������������ȫ�꼶����������Ʒ��![]() ������
������
��3��ǡ�ó���һ��һŮ�ĸ���Ϊ![]() �����̼����.
�����̼����.
��������
��1������C������ͼ�еĽǶ������ռ�ķ������ٸ���C��������5����ʽ������������������B�ļ���.
��2�����ƽ��һ�������Ʒ�������ٳ��༶�������㼴��.
��3���б��������ٸ��ݸ��ʹ�ʽ���㼴��.
(1)��������ĸ�������Ϊ��![]() (��)��B��Ʒ�ļ���Ϊ��12-2-5-2=3(��)������ͼ����
(��)��B��Ʒ�ļ���Ϊ��12-2-5-2=3(��)������ͼ����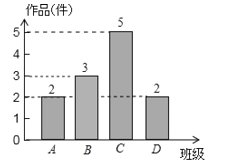
��2������ʦ�������4����ƽ����Ʒ��Ϊ��![]() ������
������
����ȫ�꼶����������Ʒ��![]() ������
������
��3���б����£�

����20�ֻ�����ȵĽ��������һ��һŮռ12�֣�
����![]() ��ǡ�ó���һ��һŮ�ĸ���Ϊ
��ǡ�ó���һ��һŮ�ĸ���Ϊ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
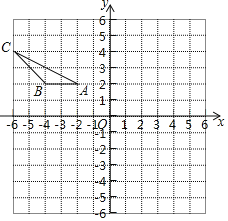
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A����2��2����B����4��2����C����6��4�����Ƚ���ABC��һȷ������ƽ�Ƶõ���A1B1C1����C�Ķ�Ӧ��Ϊ��C1�������ǣ���4����2�����ٽ���A1B1C1���Ƶ�O��ʱ����ת90��õ���A2B2C2����A1�Ķ�Ӧ��Ϊ��A2��
��1��������A1B1C1��
��2��������A2B2C2��
��3�����������α�����У���B������B1�����B2��·���ܳ����������������
��4����A2B2C2�ɿ��ɽ���ABC��ij��Ϊ��ת���ģ���ʱ����ת90����ã�����ת���ĵ��������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���OΪBC�ߵ��е㣬����У�AB2+AC2=2AO2+2BO2�������������Ͻ��ۣ�����������⣺��ͼ���ھ���DEFG�У���֪DE=4��EF=3����P����DEΪֱ���İ�Բ���˶�����PF2+PG2����СֵΪ��������

A. ![]() B.
B. ![]() C. 34 D. 10
C. 34 D. 10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ�������У�һ�κ���y����4x+4��ͼ����x�ᡢy��ֱ���A��B����.������ABCD�Ķ���C��D�ڵ�һ���ޣ�����D�ڷ���������![]() ��k��0����ͼ����.��������ABCD����ƽ��n����λ����Cǡ�����ڷ�����������ͼ���ϣ���n��ֵ��_____.
��k��0����ͼ����.��������ABCD����ƽ��n����λ����Cǡ�����ڷ�����������ͼ���ϣ���n��ֵ��_____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1��������ABCD��һ��BC��ֱ������ϵ��x���ϣ��۵���AD,ʹ��D����x���ϵ�F�����ۺ�ΪAE����֪AB=8��AD=10�������B����Ϊ��m,0��������m��0.
��1�����E��F�����꣨�ú�m��ʽ�ӱ�ʾ������5�֣�
��2������OA������OAF�ǵ��������Σ���m��ֵ����4�֣�
��3����ͼ��2������������y=a(x��m��6)2+h����A��E���㣬�䶥��ΪM������AM������OAM=90�㣬��a��h��m��ֵ. ��5�֣�
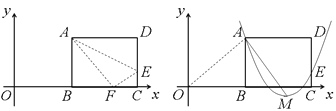
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȫ������ÿ�춼�ܹ�������״������Ⱦ����ȫ������ͺ������飬������2020��2��7��С�������Ͽ�����2020��2��6���й�ȫ�����人������ͳ��ͼ����
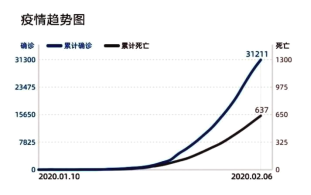
ͼ1ȫ����������ͼ
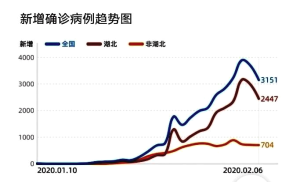
ͼ2����ȷ�ﲡ������ͼ
����ͳ��ͼ���ṩ����Ϣ�������ƶϲ��������ǣ� ��
A.��ͼ1�ɵó���2��6�յ�ȫ��ȷ�ﲡ���ﵽ3��࣬�����ǵ���ȷ�ﲡ������5327���������ɱ���˵������״���������ǵ���������Ⱦ��ǿ��
B.��ͼ2�ɵó���2��6���������������½���˵����ʱȫ�����ۼ�ȷ�ﲡ����ʼ�½�����������õ����ƣ�����������ķ��߹�������������Ч
C.��ͼ2��2��6���������������½������Թ���2��6�պ�ȫ������״���������ۼ�ȷ�ﲡ���ĵ��������ʻ����10%��
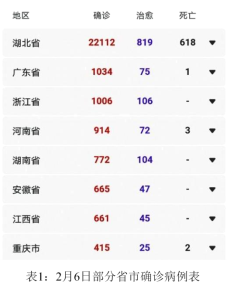
D.�ӱ�1�ɿ���ȷ�ﲡ���϶��ʡ�дֶ����ں�����Χ���ܴ�ԭ��������Я�������������˿���ɵģ����Կ����������Ч�ֶ����ڼҸ��룬ͬʱҲ�����ƶ����½��������������������Ի��ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c��a��0����y�ύ�ڵ�C����x�ύ��A��B���㣬���е�B������ΪB��4��0���������ߵĶԳ��ύx���ڵ�D��CE��AB�����������ߵĶԳ��ύ�ڵ�E���������н��ۣ���a��0����b��0����4a+2b+c��0����AD+CE��4������������ȷ���۵�����ǡ�_____________________ ����
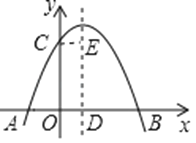
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��ͼ��������������
��ͼ��������������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
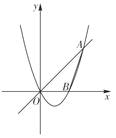
��1���������ߵĽ���ʽ��
��2����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ���������߶Գ������Ƿ���ڵ�
���������߶Գ������Ƿ���ڵ�![]() ��ʹ
��ʹ![]() ����Сֵ�������ڣ��������
����Сֵ�������ڣ��������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com