
【题目】完成下面的推理过程.
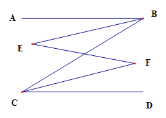
如图,AB∥CD,BE、CF分别是∠ABC和∠BCD的平分线.求证:∠E=∠F
证明:∵AB∥CD(已知)
∴∠ABC=∠BCD( )
∵BE、CF分别是∠ABC和∠BCD的平分线(已知)
∴∠CBE=![]() ∠ABC,∠BCF=
∠ABC,∠BCF=![]() ∠BCD( )
∠BCD( )
∴∠CBE=∠BCF( )
∴BE∥CF( )
∴∠E=∠F( )
科目:初中数学 来源: 题型:
【题目】如图,是由若干个完全相同的小正方体组成的一个几何体。
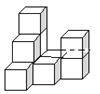
(1)图中有 块小正方体;
(2)请画出这个几何体的左视图和俯视图;(用阴影表示)
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和左视图不变,那么最多可以再添加几个小正方体?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产150辆自行车,平均每天生产辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正、减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产 辆;
(2)产量最多的一天比生产量最少的一天多生产 辆;
(3)该厂实行计划工资制,每辆车![]() 元,超额完成任务每辆奖
元,超额完成任务每辆奖![]() 元,少生产一辆扣
元,少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少?
元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上任意两点之间的距离均可用“右﹣左”表示,即右边的数(较大)减去左边的数(较小).已知数轴上两点A、B对应的数分别为﹣2、5,则A、B两点之间的距离记为AB,且AB=5﹣(﹣2)=7.P为数轴上的动点,其对应的数为x.
![]()
(1)若点P到A,B两点的距离相等,写出点P对应的数;
(2)数轴上是否存在点P,使点P到A,B两点的距离之和为11,若存在,请求出x的值;若不存在,请说明理由;
(3)若点P在原点,现在A,B,P三个点均向左匀速运动,其中点P的速度为每秒1个单位;A,B两点中有一个点速度与点P的速度一致,另一个点以每秒3单位的速度运动;则几秒后点P到A,B两点的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分类讨论是一种非常重要的数学方法,如果一道题提供的已知条件中包含几种情况,我们可以分情况讨论来求解.例如:已知点A,B,C在一条直线上,若AB=8,BC=3则AC长为多少?
通过分析我们发现,满足题意的情况有两种:情况当点C在点B的右侧时,如图1,此时,AC=11;

情况②当点C在点B的左侧时, 如图2此时,AC=5.

仿照上面的解题思路,完成下列问题:
问题(1): 如图,数轴上点A和点B表示的数分别是-1和2,点C是数轴上一点,且BC=2AB,则点C表示的数是.
![]()
问题(2): 若![]() ,
,![]() 求
求![]() 的值.
的值.
问题(3): 点O是直线AB上一点,以O为端点作射线OC、OD,使![]() ,
,![]() ,求
,求![]() 的度数(画出图形,直接写出结果).
的度数(画出图形,直接写出结果).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC=CD=AD=4,∠DAB=∠B=∠C=∠D=90°,E,F分别是边BC,CD上的点,且CE=![]() BC,F为CD的中点,问△AEF是什么三角形?请说明理由.
BC,F为CD的中点,问△AEF是什么三角形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《道德经》中的“道生一,一生二,二生三,三生万物”道出了自然数的特征,在数的学习过程中,我们会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数,合数等,现在我们来研究另一种特珠的自然数“纯数”.
定义:对于自然数![]() ,在计算
,在计算![]() 时,各数位都不产生进位,则称这个自然数
时,各数位都不产生进位,则称这个自然数![]() 为“纯数”,例如:32是“纯数”,因为计算
为“纯数”,例如:32是“纯数”,因为计算![]() 时,各数位都不产生进位;23不是“纯数”,因为计算
时,各数位都不产生进位;23不是“纯数”,因为计算![]() 时,个位产生了进位.
时,个位产生了进位.
(1)判断2019和2020是否是“纯数”?请说明理由;
(2)求出不大于100的“纯数”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题:
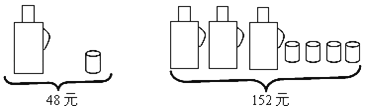
(1)一个水瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和n(n>10,且n为整数)个水杯,请问选择哪家商场购买更合算,并说明理由.(必须在同一家购买)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 同时从点
同时从点![]() 出发,以相同的速度分别沿折线
出发,以相同的速度分别沿折线![]() 、射线
、射线![]() 运动,连接
运动,连接![]() .当点
.当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 同时停止运动.设
同时停止运动.设![]() ,
,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
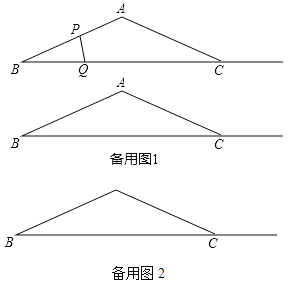
(1)求![]() 长;
长;
(2)求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(3)请直接写出![]() 为等腰三角形时
为等腰三角形时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com