
【题目】如图,分别延长□ABCD的边CD,AB到E,F,使DE=BF,连接EF,分别交AD,BC于G,H,连结CG,AH.
求证:CG∥AH.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是安装在斜屋面上的热水器,图2是安装该热水器的侧面示意图.已知,斜屋面的倾角为25°,长为2.1米的真空管AB与水平线AD的夹角为40°,安装热水器的铁架水平横管BC长0.2米,求铁架垂直管CE的长(结果精确到0.01米). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
我们已经学习了一元二次方程的多种解法:如因式分解法,开平方法,配方法和公式法,还可以运用十字相乘法,请从以下一元二次方程中任选两个,并选择你认为适当的方法解这个方程.
①![]() ②
②![]() ③
③![]() ④
④![]()
我选择第 个方程。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知小正方形 ABCD 的面积为1,把它的各边延长一倍得到新正方形 A 1 B 1 C 1 D 1 ;把正方形 A 1 B 1 C 1 D 1 边长按原法延长一倍得到正方形 A 2 B 2 C 2 D 2 (如图(2));以此下去,则正方形 A n B n C n D n 的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵ ,
∴∠CDA=90°,∠DAB=90° ( ).
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴ ( ),
∴DF∥AE ( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
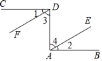
【题目】如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵ ,
∴∠CDA=90°,∠DAB=90° ( ).
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴ ( ),
∴DF∥AE ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,AO⊥BC,DO⊥OE.
(1)不添加其他条件情况下,请尽可能多地写出图中有关角的等量关系(至少3个);
(2)如果∠COE ![]() 350,求∠BOD的度数.
350,求∠BOD的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com