
 为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边有总长为40m的栅栏围住,如图所示,若设绿化带的BC边长为xm,绿化带的面积为ym2,则y与y之间的函数表达式是y=$-\frac{1}{2}{x}^{2}$+20x,y取20时,y取得最大值是200.
为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边有总长为40m的栅栏围住,如图所示,若设绿化带的BC边长为xm,绿化带的面积为ym2,则y与y之间的函数表达式是y=$-\frac{1}{2}{x}^{2}$+20x,y取20时,y取得最大值是200. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
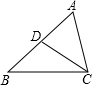 如图所示,在下列给出的条件中,不能够判定△ABC∽△ACD的是( )
如图所示,在下列给出的条件中,不能够判定△ABC∽△ACD的是( )| A. | ∠B=∠ACD | B. | ∠ADC=∠ACB | C. | AC2=AD•AB | D. | $\frac{AC}{CD}$=$\frac{AB}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
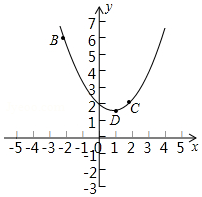 在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.
在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
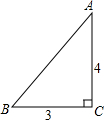 如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片折叠:使点A落在B处.这折叠的折痕长$\frac{15}{8}$.
如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片折叠:使点A落在B处.这折叠的折痕长$\frac{15}{8}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com