Question

阅读下题和分析过程，并按要求进行证明．

如图所示，已知在四边形ABCD中，AB=DC，AC=BD，AD≠BC．

求证：四边形ABCD是等腰梯形．

分析：要证四边形ABCD是等腰梯形，因为AB=DC，所以只要证四边形ABCD是梯形即可；又因为AD≠BC，故只需证AD∥BC即可；要证AD∥BC，现有如图所示四种添加辅助线的方法，请任意选择其中两种图形对原题进行证明．

Answer 1

答案：略
解析：

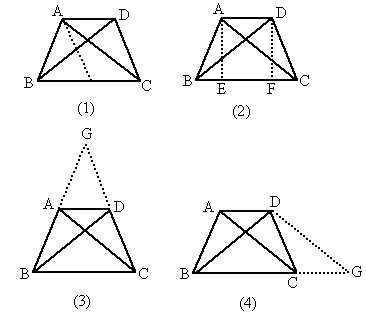
选(3)．延长BA，CD交于点G．∵AB=DC，AC=BD，AD=AD，∴△ABD≌△DCA，∴∠ABD=∠DCA．∵∠G=∠G，∴△BDG≌△CAG，∴AG=GD，∴∠DAG=∠ADG，∴BG=CG，∴∠CBG=∠BCG．∵∠G=∠G，∴∠DAG=∠CBG，∴AD∥BC．∵AD≠BC，∴AB不平行CD，∴四边形ABCD是等腰梯形． 选(4)．过点D作DG∥AC交BC延长线于点G，∴∠G=∠ACB．∵AB=DC，AC=BD，BC=BC，∴△ABC≌△DCB，∴∠DBC=∠ACB，∴∠DBC=∠G，∴BD=DG，∴DG=AC，∴四边形ACGD是平行四边形，∴AD∥BG．∵AD≠BC，∴AB不平行CD．∴四边形ABCD是等腰梯形．