
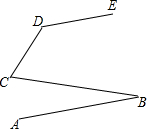
 如图,AB∥DE,∠BCD=65°,∠CDE=135°,问∠ABC等于多少度?为什么?
如图,AB∥DE,∠BCD=65°,∠CDE=135°,问∠ABC等于多少度?为什么?  53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:填空题
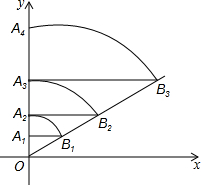 如图,直线l:y=$\frac{\sqrt{3}}{3}$x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2,再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,照此做法进行下去,点A2017的坐标为(0,22016).
如图,直线l:y=$\frac{\sqrt{3}}{3}$x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2,再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,照此做法进行下去,点A2017的坐标为(0,22016).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 年龄组 | 12岁 | 13岁 | 14岁 | 15岁 |
| 参赛人数 | 5 | 19 | 13 | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 | 2 | 8 | 10 | 17 | 6 |
| 13 | 7 | 5 | 7 | 3 | 12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
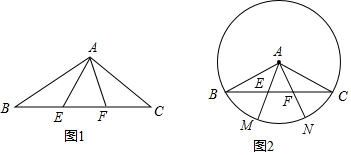
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
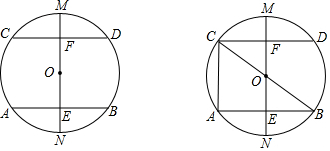
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com