
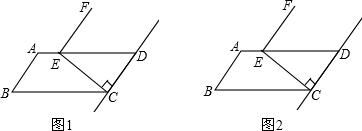
在□ABCD中,过点C作CE⊥CD交AD于点E,将线段EC绕点E逆时针旋转90°得到线段EF(如图)
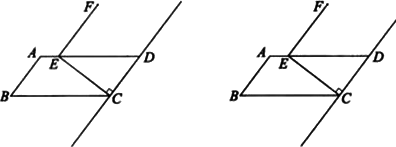
(1)在图中画图探究:
①当P为射线CD上任意一点(P1不与C重合)时,连结EP1绕点E逆时针旋转90°得到线段EC1.判断直线FC1与直线CD的位置关系,并加以证明;
②当P2为线段DC的延长线上任意一点时,连结EP2,将线段EP2绕点E逆时针旋转90°得到线段EC2.判断直线C1C2与直线CD的位置关系,画出图形并直接写出你的结论.
(2)若AD=6,tanB=![]() ,AE=1,在①的条件下,设CP1=x,S△P1FC1=y,求y与x之间的函数关系式,并写出自变量x的取值范围.
,AE=1,在①的条件下,设CP1=x,S△P1FC1=y,求y与x之间的函数关系式,并写出自变量x的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 90°得到线段EG2.判断直线G1G2与直线CD的位置关系,画出图形并直接写出你的结论.
90°得到线段EG2.判断直线G1G2与直线CD的位置关系,画出图形并直接写出你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在?ABCD中,过点B作BE⊥CD,垂足为E,连接AE.F为AE上一点,且∠BFE=∠C.
如图,在?ABCD中,过点B作BE⊥CD,垂足为E,连接AE.F为AE上一点,且∠BFE=∠C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com