
 .
.
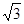 ) -----------2分
) -----------2分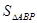 =2
=2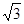 -t (0≤t≤
-t (0≤t≤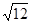 ) -----------4分
) -----------4分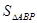 =t-
=t-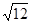 (t>
(t>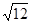 ) -----------6分
) -----------6分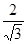 ), (1,
), (1,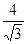 ), (3,
), (3, 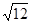 ) -----------8分
) -----------8分
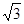 ,OA=1.
,OA=1.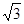 ).
).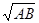 =12+(
=12+(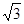 )2=2,
)2=2,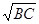 =(
=(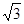 )2+(3)2=2
)2+(3)2=2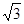 ,
,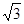 )2=16=AC2.
)2=16=AC2.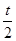 ,
,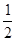 ×4×
×4×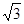 -
-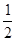 ×4×
×4×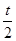 = 2
= 2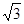 -t(0≤t< 23).
-t(0≤t< 23).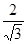 ), (1,
), (1,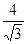 ), (3,
), (3, 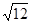 )
)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:单选题
| A.x<-2 | B.-2<x<-1 | C.-2<x<0 | D.-1<x<0 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
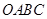 的两顶点
的两顶点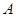 、
、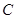 分别在
分别在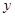 轴、
轴、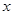 轴的正半轴上,点
轴的正半轴上,点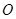 在原点.现将正方形
在原点.现将正方形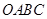 绕
绕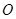 点顺时针旋转,旋转角为θ,当
点顺时针旋转,旋转角为θ,当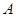 点第一次落在直线
点第一次落在直线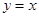 上时停止旋转.旋转过程中,
上时停止旋转.旋转过程中, 边交直线
边交直线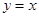 于点
于点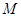 ,
,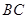 边交
边交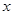 轴于点
轴于点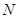 .
.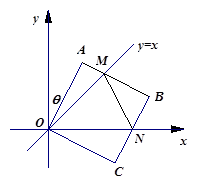
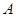 点第一次落在直线
点第一次落在直线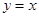 上时,求A、B两点坐标(直接写出结果);
上时,求A、B两点坐标(直接写出结果);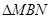 的周长为
的周长为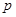 ,在旋转正方形
,在旋转正方形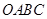 的过程中,
的过程中,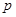 值是否有变化?请证明你的结论.
值是否有变化?请证明你的结论.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ;
;| A.①② | B.②③ | C.①②③ | D.①③ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (千克)与零售价
(千克)与零售价 (元/千克)之间的函数关系式;
(元/千克)之间的函数关系式; (千克)为整数,零售价
(千克)为整数,零售价 (元/千克)满足条件5<
(元/千克)满足条件5< <5.1
<5.1

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com