
分析 (1)设去年每吨大蒜的平均价格是x元,则第一次采购的平均价格为(x+500)元,第二次采购的平均价格为(x-500)元,根据第二次的采购数量是第一次采购数量的两倍,据此列方程求解;
(2)先求出今年所采购的大蒜数,根据采购的大蒜必需在30天内加工完毕,蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半,据此列不等式组求解,然后求出最大利润.
解答 解:(1)设去年每吨大蒜的平均价格是x元,
由题意得,$\frac{400000}{x+500}$×2=$\frac{600000}{x-500}$,
解得:x=3500,
经检验:x=3500是原分式方程的解,且符合题意,
答:去年每吨大蒜的平均价格是3500元;
(2)由(1)得,今年的大蒜数为:$\frac{400000}{4000}$×3=300(吨),
设应将m吨大蒜加工成蒜粉,则应将(300-m)吨加工成蒜片,
由题意得,$\left\{\begin{array}{l}{m≥\frac{300-m}{2}}\\{\frac{m}{8}+\frac{300-m}{12}≤30}\end{array}\right.$,
解得:100≤m≤120,
总利润为:1000m+600(300-m)=400m+180000,
当m=120时,利润最大,为228000元.
答:应将120吨大蒜加工成蒜粉,最大利润为228000元.
点评 本题考查了分式方程和一元一次不等式的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
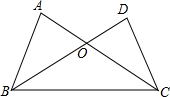 如图,下列条件中,不能证明△ABC≌△DCB的是( )
如图,下列条件中,不能证明△ABC≌△DCB的是( )| A. | AB=DC,AC=DB | B. | AB=DC,∠ABC=∠DCB | C. | BO=CO,∠A=∠D | D. | AB=DC,∠DBC=∠ACB |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 知识迁移
知识迁移查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.8 | B. | 4.8或3.8 | C. | 3.8 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.25×109 | B. | 2.25×108 | C. | 22.5×107 | D. | 225×106 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com