
【题目】A、B两地相距216千米,甲、乙分别在A、B两地,若甲骑车的速度为15千米/时,乙骑车的速度为12千米/时。.
(1)甲、乙同时出发,背向而行,问几小时后他们相距351千米?
(2)甲、乙相向而行,甲出发三小时后乙才出发,问乙出发几小时后两人相遇?
(3)甲、乙相向而行,要使他们相遇于AB的中点,乙要比甲先出发几小时?
(4)甲、乙同时出发,相向而行,甲到达B处,乙到达A处都分别立即返回,几小时后相遇?相遇地点距离A有多远?
【答案】(1) 5;(2)![]() ;(3) 1.8小时;(4) 24小时后相遇地点距离A有72千米.
;(3) 1.8小时;(4) 24小时后相遇地点距离A有72千米.
【解析】试题分析:根据相遇问题的等量关系为:两者的路程之和=相距总路程,设未知数,列方程求解即可.
试题解析:解:(1)设经过x小时后他们相距351千米,根据题意得:
15x+12x=351-216
解得:x=5
答:经过5小时后他们相距351千米.
(2)设相向而行,乙出发x小时后两人相遇,根据题意得:
15(3+x)+12x=216
解得:x=![]() .
.
答:乙出发![]() 小时后两人相遇.
小时后两人相遇.
(3)到达AB的中点甲需要的时间=216÷2÷15=7.2(小时),乙需要的时间=216÷2÷12=9(小时),故乙要比甲先出发的时间=9-7.2=1.8(小时);
答:乙要比甲先出发1.8小时.
(4)设经过x小时返回路上相遇.∵返回时相遇,∴总路程为3个AB的距离,∴(15+12)x=216×3
解得:x=24(小时)
此时离A处的距离=12×24-216=72(千米).
答:经过24小时返回路上相遇,相遇地点距离A有72千米.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】一个多边形截去一个角(不过顶点)后,形成的多边形的内角和是2520°,那么原多边形的边数是( )
A. 13 B. 14 C. 15 D. 13或15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是________(写成两数平方差的形式);

(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是________,长是________,面积是________(写成多项式乘法的形式);
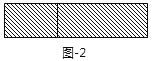
(3)比较左、右两图的阴影部分面积,可以得到乘法公式________(用式子表达).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列关于a的单项式,探究其规律:a,3a2,5a3,7a4,9a5,….按照上述规律,第2019个单项式是( )
A. 2019a2019B. 4039a2019C. 4038a2019D. 4037a2019
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:![]() ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.

(1)山坡坡角(即∠ABC)的度数等于 度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
(1)试判断△BEC是否为等腰三角形,请说明理由?
(2)若AB=1,∠ABE=45°,求BC的长;
(3)在原图中画△FCE,使它与△BEC关于CE的中点O成中心对称,此时四边形BCFE是什么特殊平行四边形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点O是AC与BD的交点,过点O的直线EF与AB、CD的延长线分别交于点E、F.
(1)求证:△BOE≌△DOF
(2)当EF⊥AC时,四边形AECF是怎样的特殊四边形?证明你的结论
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com