
【题目】如图,在四边形ABCD中,AB=AD,∠C=90°,以AB为直径的⊙O交AD于点E,CD=ED,连接BD交⊙O于点F.
(1)求证:BC与⊙O相切;
(2)若BD=10,AB=13,求AE的长.
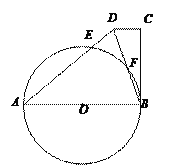
【答案】(1)见解析;(2)![]()
【解析】分析:(1)连接BE,可证明Rt△BCD≌Rt△BED,结合条件可证明∠BDC=∠ABD,可证得AB∥CD,最后看单词结果;(2)连接EF,根据圆周角定理得出∠AFB=90°,在Rt△ABF中根据勾股定理得出BF=5,然后由Rt△ABF∽Rt△BDC,ED= ,从而求出AE的长.
详解:(1)证明:连接BE.
∵ AB是直径,
∴∠AEB=90°.
在Rt△BCD和Rt△BED 中
![]()
∴Rt△BCD≌Rt△BED.
∴∠ADB=∠BDC.
又 AD=AB,
∴∠ADB=∠ABD.
∴∠BDC=∠ABD.
∴AB∥CD.
∴∠ABC+∠C=180°.
∴∠ABC=180°-∠C=180°―90°=90°.
即BC⊥AB.
又B在⊙O上,
∴BD与⊙O相切.
(2)解:连接AF.
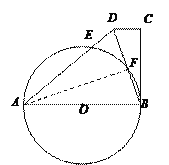
∵AB是直径,
∴∠AFB=90°,即AF⊥BD.
∵AD=AB,BC=10,
∴BF=5.
在Rt△ABF和Rt△BDC中
![]()
∴Rt△ABF∽Rt△BDC.
∴![]() =
=![]() .
.
∴![]() =
=![]() .
.
∴DC=![]() .
.
∴ED=![]() .
.
∴AE=AD―ED=13―![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法中:
①在Rt△ABC中,∠C=90°,CD为AB边上的中线,若CD=2,则AB=4;
②八边形的内角和度数为1080°;
③2、3、4、3这组数据的方差为0.5;
④分式方程![]() =
=![]() 的解为x=
的解为x=![]() ;
;
⑤已知菱形的一个内角为60°,一条对角线为2,则另一对角线为2![]() .
.
正确的序号有( )
A. ①②③⑤ B. ①②③④ C. ①③④⑤ D. ②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
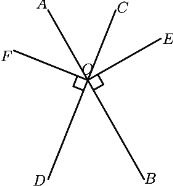
【题目】已知:如图直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]()
(1)图中与![]() 互余的角有 ,图中与
互余的角有 ,图中与![]() 互补的角有 (备注:写出所有符合条件的角)
互补的角有 (备注:写出所有符合条件的角)
(2)根据下列条件,分别求![]() 的度数:①射线
的度数:①射线![]() 平分
平分![]() ;②
;②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:
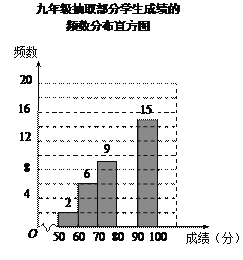
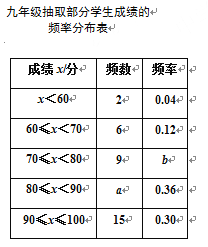
请根据所给信息,解答下列问题:
(1)a=______,b=_______;
(2)请补全频数分布直方图;
(3)已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)

查看答案和解析>>
科目:初中数学 来源: 题型:
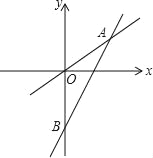
【题目】如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB.
(1)求这两个函数的解析式;
(2)求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小烨在探究数轴上两点间距离时发现:若![]() 两点在
两点在![]() 轴上或与
轴上或与![]() 轴平行,
轴平行,![]() 两点的横坐标分别为
两点的横坐标分别为![]() ,则
,则![]() 两点间距离为
两点间距离为![]() ;若
;若![]() 两点在
两点在![]() 轴上或与
轴上或与![]() 轴平行,
轴平行,![]() 两点的纵坐标分别为
两点的纵坐标分别为![]() ,则
,则![]() 两点间距离为
两点间距离为![]() .据此,小烨猜想:对于平面内任意两点
.据此,小烨猜想:对于平面内任意两点![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
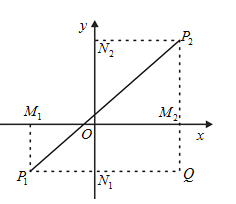
(1)请你利用下图,试证明:;
(2)若![]() ,试在
,试在![]() 轴上求一点
轴上求一点![]() ,使
,使![]() 的距离最短,并求出
的距离最短,并求出![]() 的最小值和
的最小值和![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
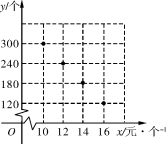
【题目】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量![]() (单位:个)与销售单价
(单位:个)与销售单价![]() (单位:元/个)之间的对应关系如图所示:
(单位:元/个)之间的对应关系如图所示:
(1) ![]() 与
与![]() 之间的函数关系是 .
之间的函数关系是 .
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润![]() (单位:元)与销售单价
(单位:元)与销售单价![]() (单位:元/个)之间的函数关系式;
(单位:元/个)之间的函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com