
【题目】某品牌笔记本电脑的售价是5000元/台。最近,该商家对此型号笔记本电脑举行促销活动,有两种优惠方案。方案一:每台按售价的九折销售,方案二:若购买不超过5台,每台按售价销售;若超过5台,超过的部分每台按售价的八折销售。设公司一次性购买此型号笔记本电脑x合、
(I)根据题意,填写下表:

(II)设选择方案一的费用为y1元,选择方案二的费用为为y2元,分别写出y1,y2关于x的函数关系式;
(III)当x>15时,该公司采用哪种方案购买更合算?并说明理由
【答案】(1)45000,85000,
(2)y1=4500x(x≥0),当0≤x≤5时,y2=5000x,当x>5时,y2=5000+4000x;(3)方案二购买更合算
【解析】
(1)(2)根据题意可写出方案一的费用y1,方案二的费用y2的函数关系式,即可进行求解;(3)令y= y1- y2,根据新的函数关系式来判断选择哪个方案合算.
(1)用方案二购买10台时,费用为5×5000+(10-5)×5000×80%=45000,
用方案二购买20台时,费用为5×5000+(20-5)×5000×80%=85000,
(2)依题意得y1=5000×90%x=4500x(x≥0)
当0≤x≤5时,y2=5000x,
当x>5时,y2=5000×5+0.8(x-5)×5000=5000+4000x;
(3)令y= y1- y2=4500x-5000-4000x=500x-5000,
当x=15时,y>0,∴y随x的增大而增大,
∴当x>15时,y>0,
即y1> y2
∴方案二购买更合算


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】(1)操作发现:如图①,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是__________;位置关系是__________.
(2)类比思考:
如图②,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其它条件不变,小明发现的上述结论还成立吗?请说明理由.
(3)深入研究:
如图③,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其它条件不变,试判断△GMN的形状,并给与证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
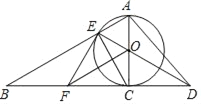
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,作OF∥AB交BC于点F,连接EF.
(1)求证:OF⊥CE;
(2)求证:EF是⊙O的切线;
(3)若⊙O的半径为3,∠EAC=60°,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南某中学在参加“创文明城,点赞泉城”书画比赛中,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作鼎的数量进行了分析统计,制作了两幅不完整的统计图.
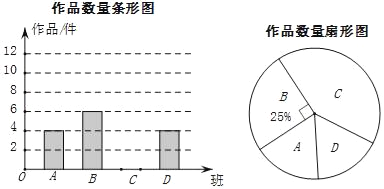
请根据以上信息,回答下列问题:
(l)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请补充完整条形统计图,并计算扇形统计图中C班作品数量所对应的圆心角度数 .
(3)请估计全校共征集作品的什数.
(4)如果全枝征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一样等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
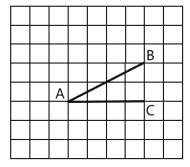
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上。
(I)AB的长度等于
(II)请你在图中找到一个点P,使得AB是∠PAC的角平分线请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
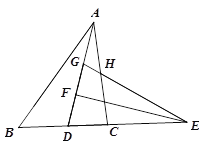
【题目】如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的袋子中装有4个相同的小球,它们除颜色外无其它差别,把它们分别标号:1、2、3、4,
(1)随机摸出一个小球后,放回并摇匀,再随机摸出一个,用列表或画树状图的方法求出“两次取的球标号相同”的概率
(2)随机摸出两个小球,直接写出“两次取出的球标号和等于4”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,﹣3).
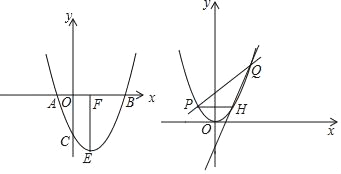
(1)求抛物线的解析式;
(2)如图1,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
(3)如图2,将抛物线平移,使其顶点E与原点O重合,直线y=kx+2(k>0)与抛物线相交于点P、Q(点P在左边),过点P作x轴平行线交抛物线于点H,当k发生改变时,请说明直线QH过定点,并求定点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一张矩形纸片ABCD,![]() ,
,![]() .
.
![]() 如图1,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为
如图1,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为![]() 点M,N分别在边AD,BC上
点M,N分别在边AD,BC上![]() ,利用直尺和圆规画出折痕
,利用直尺和圆规画出折痕![]() 不写作法,保留作图痕迹
不写作法,保留作图痕迹![]() ;
;
![]() 如图2,点K在这张矩形纸片的边AD上,
如图2,点K在这张矩形纸片的边AD上,![]() ,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点
,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点![]() ,
,![]() 处,小明认为
处,小明认为![]() 所在直线恰好经过点D,他的判断是否正确,请说明理由.
所在直线恰好经过点D,他的判断是否正确,请说明理由.
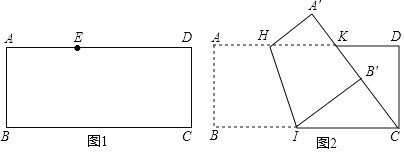
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com