
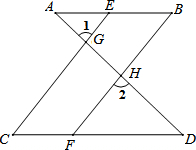
 如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:分析 首先确定∠1=∠CGD是对顶角,利用等量代换,求得∠2=∠CGD,则可根据:同位角相等,两直线平行,证得:CE∥BF,又由两直线平行,同位角相等,证得角相等,易得:∠BFD=∠B,则利用内错角相等,两直线平行,即可证得:AB∥CD.
解答 解:∵∠1=∠2(已知),
且∠1=∠CGD(对顶角相等),
∴∠2=∠CGD(等量代换),
∴CE∥BF(同位角相等,两直线平行),
∴∠C=∠BFD(两直线平行,同位角相等),
又∵∠B=∠C(已知),
∴∠BFD=∠B(等量代换),
∴AB∥CD(内错角相等,两直线平行).
故答案为:(对顶角相等),(同位角相等,两直线平行),C,(两直线平行,同位角相等),(内错角相等,两直线平行).
点评 本题主要考查了平行线的判定与性质.注意数形结合思想的应用是解答此题的关键.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+5y=2}\\{xy=7}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+\frac{1}{y}=1}\\{3x-5y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x=5y}\\{\frac{y}{4}-\frac{z}{3}=\frac{4}{5}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-3=9}\\{x+4y=17}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 成绩(分) | 46 | 48 | 49 | 50 |
| 人数(人) | 2 | 1 | 2 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com