
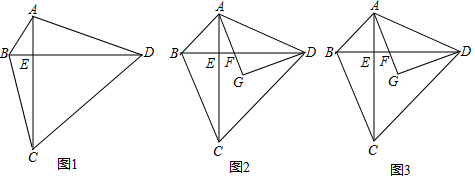
分析 (1)由已知得出点A、B、C、D四点共圆,由圆周角定理证出∠ABD=∠ACD,由等腰三角形的性质得出∠GAD=∠GDA,∠AGD=2∠ABD,由三角形内角和定理得出∠ABD+∠GAD=90°,∠ABD+∠BAC=90°,即可得出∠BAC=∠GAD;
(2)由等腰三角形的性质得出∠CAD=∠CDA,由∠BAC=∠BDC=∠GAD,得出∠EAF=∠ADF,再由三角形的外角性质得出∠BAF=∠BFA,即可得出结论;
(3)设BE=3x,则EF=2x,BA=BF=5x,由勾股定理得出AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=4x,由相交弦定理得出:AE•CE=BE•DE,求出CE=$\frac{3}{2}$x+9,得出CD=CA=4x+$\frac{3}{2}$x+9=$\frac{11}{2}$x+9,在Rt△CDE中,由勾股定理得出方程,解方程求出x的值,即可得出AB的长.
解答 (1)证明:∵∠BAC=∠BDC,
∴点A、B、C、D四点共圆,
∴∠ABD=∠ACD,
∵AG=DG,∠AGD=2∠ACD.
∴∠GAD=∠GDA,∠AGD=2∠ABD,
∵∠AGD+2∠GAD=180°,
∴2∠ABD+2∠GAD=180°,
∴∠ABD+∠GAD=90°,
又∵AC⊥BD,
∴∠ABD+∠BAC=90°,
∴∠BAC=∠GAD;
(2)证明:∵CA=CD,
∴∠CAD=∠CDA,
∵∠BAC=∠BDC=∠GAD,
∴∠EAF=∠ADF,
∵∠BAF=∠BAC+∠EAF,∠BFA=∠GAD+∠ADF,
∴∠BAF=∠BFA,
∴BA=BF;
(3)解:∵BE:EF=3:2,
设BE=3x,则EF=2x,
∴BA=BF=5x,
∵AC⊥BD,
∴AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=4x,
∵点A、B、C、D四点共圆,
∴由相交弦定理得:AE•CE=BE•DE,即4x•CE=3x•(2x+12),
∴CE=$\frac{3}{4}$(2x+12)=$\frac{3}{2}$x+9,
∴CD=CA=4x+$\frac{3}{2}$x+9=$\frac{11}{2}$x+9,
在Rt△CDE中,由勾股定理得:($\frac{3}{2}$x+9)2+(2x+12)2=($\frac{11}{2}$x+9)2,
解得:x=2,或x=-3(舍去),
∴AB=5x=10.
点评 本题时四边形综合题目,考查了四点共圆、圆周角定理、等腰三角形的性质与判定、三角形内角和定理、三角形的外角性质、勾股定理、相交弦定理等知识;本题综合性强,难度较大,特别是(3)中,需要运用相交弦定理和勾股定理得出方程才能得出结果.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是半圆O的直径,射线AM、BN分别与半圆O相切于点A、B,点E在半圆上,点D在射线AM上,连接DE并延长交射线BN于点C,连接AE并延长交射线BN于点G.
如图,AB是半圆O的直径,射线AM、BN分别与半圆O相切于点A、B,点E在半圆上,点D在射线AM上,连接DE并延长交射线BN于点C,连接AE并延长交射线BN于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
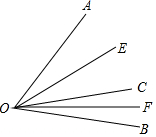 已知,如图,OC是∠AOB内部一条射线,∠AOB=60°,OE、OF分别是∠AOC、∠COB的角平分线,求∠EOF的度数?如果设∠AOB=β,其他条件不变,你能猜测出∠EOF的大小吗?请用一句简洁的话表述你发现的规律.
已知,如图,OC是∠AOB内部一条射线,∠AOB=60°,OE、OF分别是∠AOC、∠COB的角平分线,求∠EOF的度数?如果设∠AOB=β,其他条件不变,你能猜测出∠EOF的大小吗?请用一句简洁的话表述你发现的规律.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com