
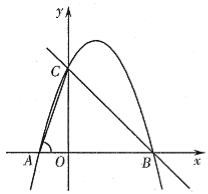
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЮЊзјБъдЕуЃЌжБЯпy=Љx+nгыxжсЁЂyжсЗжБ№НЛгкBЁЂCСНЕуЃЌХзЮяЯпy=ax2+bx+3(aЁй0)Й§CЁЂBСНЕуЃЌНЛxжсгкСэвЛЕуAЃЌСЌНгACЃЌЧвtanЁЯCAO=3ЃЎ
(1)ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
(2)ШєЕуPЪЧЩфЯпCBЩЯвЛЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпЃЌДЙзуЮЊHЃЌНЛХзЮяЯпгкQЃЌЩшPЕуКсзјБъЮЊtЃЌЯпЖЮPQЕФГЄЮЊdЃЌЧѓГіdгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІЕФздБфСПtЕФШЁжЕЗЖЮЇЃЛ
(3)дк(2)ЕФЬѕМўЯТЃЌЕБЕуPдкЯпЖЮBCЩЯЪБЃЌЩшPH=eЃЌвбжЊdЃЌeЪЧвдyЮЊЮДжЊЪ§ЕФвЛдЊЖўДЮЗНГЬЃКy2Ѓ(m+3)y+![]() (5m2Ѓ2m+13)=0 (mЮЊГЃЪ§)ЕФСНИіЪЕЪ§ИљЃЌЕуMдкХзЮяЯпЩЯЃЌСЌНгMQЁЂMHЁЂPMЃЌЧвЃЎMPЦНЗжЁЯQMHЃЌЧѓГіtжЕМАЕуMЕФзјБъЃЎ
(5m2Ѓ2m+13)=0 (mЮЊГЃЪ§)ЕФСНИіЪЕЪ§ИљЃЌЕуMдкХзЮяЯпЩЯЃЌСЌНгMQЁЂMHЁЂPMЃЌЧвЃЎMPЦНЗжЁЯQMHЃЌЧѓГіtжЕМАЕуMЕФзјБъЃЎ
ЁОД№АИЁП(1) y=-x2+2x+3ЃЛ(2)  ЃЛЃЈ3ЃЉt=1, (1+
ЃЛЃЈ3ЃЉt=1, (1+![]() ЃЌ2)КЭ(1Ѓ
ЃЌ2)КЭ(1Ѓ![]() ЃЌ2).
ЃЌ2).
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉЕБx=0ЪБДњШыХзЮяЯпy=ax2+bx+3ЃЈaЁй0ЃЉОЭПЩвдЧѓГіy=3ЖјЕУГіCЕФзјБъЃЌОЭПЩвдЕУГіжБЯпЕФНтЮіЪНЃЌОЭПЩвдЧѓГіBЕФзјБъЃЌдкжБНЧШ§НЧаЮAOCжаЃЌгЩШ§НЧаЮКЏЪ§жЕОЭПЩвдЧѓГіOAЕФжЕЃЌЕУГіAЕФзјБъЃЌдйгЩД§ЖЈЯЕЪ§ЗЈНЈСЂЖўдЊвЛДЮЗНГЬзщЧѓГіЦфНтОЭПЩвдЕУГіНсТлЃЛ
ЃЈ2ЃЉЗжСНжжЧщПіЬжТлЃЌЕБЕуPдкЯпЖЮCBЩЯЪБЃЌКЭШчЭМ3ЕуPдкЩфЯпBNЩЯЪБЃЌОЭгаPЕуЕФзјБъЮЊЃЈtЃЌ-t+3ЃЉЃЌQЕуЕФзјБъЮЊЃЈtЃЌ-t2+2t+3ЃЉЃЌОЭПЩвдЕУГіdгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЖјЕУГіНсТлЃЛ
ЃЈ3ЃЉИљОнИљЕФХаБ№ЪНОЭПЩвдЧѓГіmЕФжЕЃЌОЭПЩвдЧѓГіЗНГЬЕФНтЖјЧѓЕУPQКЭPHЕФжЕЃЌбгГЄMPжСLЃЌЪЙLP=MPЃЌСЌНгLQЁЂLHЃЌШчЭМ2ЃЌбгГЄMPжСLЃЌЪЙLP=MPЃЌСЌНгLQЁЂLHЃЌОЭПЩвдЕУГіЫФБпаЮLQMHЪЧЦНааЫФБпаЮЃЌНјЖјЕУГіЫФБпаЮLQMHЪЧСтаЮЃЌгЩСтаЮЕФаджЪОЭПЩвдЧѓГіНсТлЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЕБx=0ЃЌдђy=-x+n=0+n=nЃЌy=ax2+bx+3=3ЃЌ
ЁрOC=3=nЃЎ
ЕБy=0ЃЌ
Ёр-x+3=0ЃЌx=3=OBЃЌ
ЁрBЃЈ3ЃЌ0ЃЉЃЎ
дкЁїAOCжаЃЌЁЯAOCЃН90ЁуЃЌtanЁЯCAO=![]() ЃЌ
ЃЌ
ЁрOA=1ЃЌ
ЁрAЃЈ-1ЃЌ0ЃЉЃЎ
НЋAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉДњШыy=ax2+bx+3ЃЌ
ЕУ
![]() ЃЌ
ЃЌ
НтЕУЃК![]()
ЁрХзЮяЯпЕФНтЮіЪНЃКy=-x2+2x+3ЃЛ
(2) ШчЭМ1ЃЌ
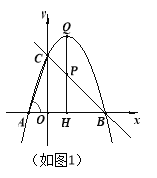
ЁпPЕуЕФКсзјБъЮЊt ЧвPQДЙжБгкxжс ЁрPЕуЕФзјБъЮЊ(tЃЌЃt+3)ЃЌ
QЕуЕФзјБъЮЊ(tЃЌЃt2+2t+3).
ЁрPQ=|(Ѓt+3)Ѓ(Ѓt2+2t+3)|=| t2Ѓ3t |
Ёр ЃЛ
ЃЛ
ЁпdЃЌeЪЧy2Ѓ(m+3)y+![]() (5m2Ѓ2m+13)=0ЃЈmЮЊГЃЪ§ЃЉЕФСНИіЪЕЪ§ИљЃЌ
(5m2Ѓ2m+13)=0ЃЈmЮЊГЃЪ§ЃЉЕФСНИіЪЕЪ§ИљЃЌ
ЁрЁїЁн0ЃЌМДЁї=(m+3)2Ѓ4ЁС![]() (5m2Ѓ2m+13)Ён0
(5m2Ѓ2m+13)Ён0
ећРэЕУЃКЁї= Ѓ4(mЃ1)2Ён0ЃЌЁпЃ4(mЃ1)2Ём0ЃЌ
ЁрЁї=0ЃЌm=1ЃЌ
Ёр PQгыPHЪЧy2Ѓ4y+4=0ЕФСНИіЪЕЪ§ИљЃЌНтЕУ![]() y1=y2=2
y1=y2=2
ЁрДЫЪБQЪЧХзЮяЯпЕФЖЅЕуЃЌ
бгГЄMPжСLЃЌЪЙLP=MPЃЌСЌНгLQЁЂLHЃЌШчЭМ2ЃЌ
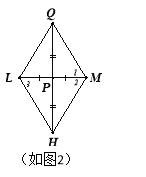
ЁпLP=MPЃЌPQ=PHЃЌЁрЫФБпаЮLQMHЪЧЦНааЫФБпаЮЃЌ
ЁрLHЁЮQMЃЌЁрЁЯ1=ЁЯ3ЃЌЁпЁЯ1=ЁЯ2ЃЌЁрЁЯ2=ЁЯ3ЃЌ
ЁрLH=MHЃЌЁрЦНааЫФБпаЮLQMHЪЧСтаЮЃЌ
ЁрPMЁЭQHЃЌЁрЕуMЕФзнзјБъгыPЕузнзјБъЯрЭЌЃЌЖМЪЧ2ЃЌ
Ёрдкy=Ѓx2+2x+3Сюy=2ЃЌЕУx2Ѓ2xЃ1=0ЃЌЁрx1=1+![]() ЃЌx2=1Ѓ
ЃЌx2=1Ѓ![]()
злЩЯЃКtжЕЮЊ1ЃЌMЕузјБъЮЊ(1+![]() ЃЌ2)КЭ(1Ѓ
ЃЌ2)КЭ(1Ѓ![]() ЃЌ2)
ЃЌ2)


 ЭЌВНСЗЯАЧПЛЏЭиеЙЯЕСаД№АИ
ЭЌВНСЗЯАЧПЛЏЭиеЙЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
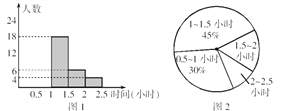
ЁОЬтФПЁПЮЊСЫМѕЧсбЇЩњЕФзївЕИКЕЃЃЌНЬг§ОжЙцЖЈЃКГѕжабЇЖЮбЇЩњУПЭэЕФзївЕзмСПВЛГЌЙ§1.5аЁЪБЃЌОХЃЈ1ЃЉАрбЇЯАЮЏдБССССЖдБОАрУПЮЛЭЌбЇЭэЩЯЭъГЩзївЕЕФЪБМфНјааСЫвЛДЮЭГМЦЃЌВЂИљОнЪеМЏЕФЪ§ОнЛцжЦСЫЯТУцСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыФуИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТУцЕФЮЪЬтЃК
ЃЈ1ЃЉИУАрЙВгаЖрЩйУћбЇЩњЃПНЋЭМ1ЕФЬѕаЮЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉМЦЫуГізївЕЭъГЩЪБМфдк1.5~2аЁЪБЕФВПЗжЖдгІЕФЩШаЮдВаФНЧЃЛ
ЃЈ3ЃЉШчЙћОХФъМЖЙВга500УћбЇЩњЃЌЧыЙРМЦОХФъМЖбЇЩњЭъГЩзївЕЪБМфГЌЙ§1.5аЁЪБЕФгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌжБЯпABЁЮDCЃЌЕуPЮЊЦНУцЩЯвЛЕуЃЌСЌНгAPгыCPЃЎ
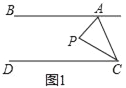
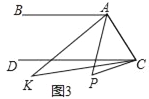
ЃЈ1ЃЉШчЭМ1ЃЌЕуPдкжБЯпABЁЂCDжЎМфЃЌЕБЁЯBAP=60ЁуЃЌЁЯDCP=20ЁуЪБЃЌЧѓЁЯAPCЃЎ
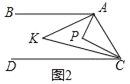
ЃЈ2ЃЉШчЭМ2ЃЌЕуPдкжБЯпABЁЂCDжЎМфЃЌЁЯBAPгыЁЯDCPЕФНЧЦНЗжЯпЯрНЛгкЕуKЃЌаДГіЁЯAKCгыЁЯAPCжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌЕуPТфдкCDЭтЃЌЁЯBAPгыЁЯDCPЕФНЧЦНЗжЯпЯрНЛгкЕуKЃЌЁЯAKCгыЁЯAPCгаКЮЪ§СПЙиЯЕЃПВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫНтбЇЩњЕФАВШЋвтЪЖЧщПіЃЌдкШЋаЃЗЖЮЇФкЫцЛњГщШЁВПЗжбЇЩњНјааЮЪОэЕїВщЃЌИљОнЕїВщНсЙћЃЌАббЇЩњЕФАВШЋвтЪЖЗжГЩЁАЕБЁЁБЁЂЁАвЛАуЁБЁЂЁАНЯЧПЁБЁЂЁАКмЧПЁБЫФИіВуДЮЃЌВЂЛцжЦГЩШчЯТСНЗљЩаВЛЭъећЕФЭГМЦЭМЃЎ

ИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉетДЮЕїВщвЛЙВГщШЁСЫ УћбЇЩњЃЌЦфжаАВШЋвтЪЖЮЊЁАКмЧПЁБЕФбЇЩњеМБЛЕїВщбЇЩњзмЪ§ЕФАйЗжБШЪЧ ЃЛ
ЃЈ2ЃЉЧыНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉИУаЃга1800УћбЇЩњЃЌЯжвЊЖдАВШЋвтЪЖЮЊЁАЕБЁЁБЁЂЁАвЛАуЁБЕФбЇЩњЧПЛЏАВШЋНЬг§ЃЌИљОнЕїВщНсЙћЃЌЙРМЦШЋаЃашвЊЧПЛЏАВШЋНЬг§ЕФбЇЩњдМга УћЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАбаЁдВаЮГЁЕиЕФАыОЖдіМг5УзЕУЕНДѓдВаЮГЁЕиЃЌДЫЪБДѓдВаЮГЁЕиЕФУцЛ§ЪЧаЁдВаЮГЁЕиЕФ4БЖЃЌЩшаЁдВаЮГЁЕиЕФАыОЖЮЊxУзЃЌШєвЊЧѓГіЮДжЊЪ§xЃЌдђгІСаГіЗНГЬ ЃЈСаГіЗНГЬЃЌВЛвЊЧѓНтЗНГЬЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
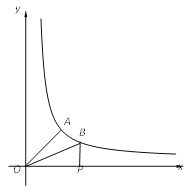
ЁОЬтФПЁПШчЭМЃЌвбжЊAЁЂBЪЧЗДБШР§КЏЪ§yЃН![]() ЭМЯѓЩЯСНЕуЃЌBPЁЭxжсЃЌДЙзуЮЊPЃЎвбжЊЁЯAOPЃН45ЁуЃЌOAЃН4ЃЌ tanЁЯBOPЃН
ЭМЯѓЩЯСНЕуЃЌBPЁЭxжсЃЌДЙзуЮЊPЃЎвбжЊЁЯAOPЃН45ЁуЃЌOAЃН4ЃЌ tanЁЯBOPЃН![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЕуAЕФзјБъЃЛ
ЃЈ2ЃЉСЌНгABЃЌЧѓЫФБпаЮAOPBЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОЙКТђвЛХњВЃСЇБКЭБЃЮТБЃЌМЦЛЎгУ2000дЊЙКТђВЃСЇБЃЌгУ2800дЊЙКТђБЃЮТБЃЎвбжЊвЛИіБЃЮТББШвЛИіВЃСЇБЙѓ10дЊЃЎИУЙЋЫОЙКТђЕФВЃСЇБгыБЃЮТБЕФЪ§СПФмЯрЭЌТ№ЃП
ЃЈ1ЃЉИљОнЬтвтЃЌМзКЭввСНЭЌбЇЖМЯШМйЩшИУЙЋЫОЙКТђЕФВЃСЇБгыБЃЮТБЕФЪ§СПФмЯрЭЌЃЌВЂЗжБ№СаГіЕФЗНГЬШчЯТЃК![]() ЃН
ЃН![]() ЃЛ
ЃЛ![]() Ѓ
Ѓ![]() ЃН10ЃЌИљОнСНЮЛЭЌбЇЫљСаЕФЗНГЬЃЌЧыФуЗжБ№жИГіЮДжЊЪ§xЃЌyБэЪОЕФвтвхЃКxБэЪО ЃЛyБэЪО ЃЛ
ЃН10ЃЌИљОнСНЮЛЭЌбЇЫљСаЕФЗНГЬЃЌЧыФуЗжБ№жИГіЮДжЊЪ§xЃЌyБэЪОЕФвтвхЃКxБэЪО ЃЛyБэЪО ЃЛ
ЃЈ2ЃЉШЮбЁЦфжавЛИіЗНГЬЫЕУїИУЙЋЫОЙКТђЕФВЃСЇБгыБЃЮТБЕФЪ§СПФмЗёЯрЭЌЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЙигкxЕФЗНГЬx2+3x+a=0гавЛИіИљЮЊЉ1ЃЌдђaЕФжЕЮЊЃЈ ЃЉ
A.2
B.Љ1
C.Љ2
D.1
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com