练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

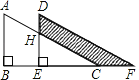
    【题目】把两个大小一样的直角三角形重叠在一起，将其中一个三角形沿着点B到C方向平移到三角形DEF的位置，AB＝9，DH＝3，平移距离为4，则阴影部分的面积是_____．

    【答案】30

    【解析】

    先判断出阴影部分面积等于梯形ABEH的面积，再根据平移变化只改变图形的位置不改变图形的形状可得DE=AB，然后求出HE，根据平移的距离求出BE=4，然后利用梯形的面积公式列式计算即可得解．

    解：∵△ABC沿着点B到点C的方向平移到△DEF的位置，

    ∴△ABC≌△DEF，

    ∴阴影部分面积等于梯形ABEH的面积，

    由平移的性质得，DE=AB，BE=4，

    ∵AB=9，DH=3，

    ∴HE=DE-DH=9-3=6，

    ∴阴影部分的面积=×（6+9）×4=30．

    故答案为：30．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，等腰直角三角形ABC的腰长为2，直角顶点A在直线l：y=2x+2上移动，且斜边BC∥x轴，当△ABC在直线l上移动时，BC的中点D满足的函数关系式为（ ）

    A. y=2x B. y=2x+1 C. y=2x+2﹣ D. y=2x﹣

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一辆大巴车在一条南北方向的道路上来回运送旅客，某一天早晨该车从A地出发，晚上到达B地，预定向北为正方向，当天行驶记录如下(单位：千米)+18，-9，+7，-14，-6，+13，-6，-8 请你根据计算回答下列问题：

    （1）B地在A地何方？相距多少千米？

    （2）该车这一天共行驶多少千米？

    （3）若该车每千米耗油0.5升，这一天共耗油多少升？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C=45°，AB的垂直平分线交AB于点E，交BC于点D；AC的垂

    直平分线交AC于点G，交BC与点F，连接AD、AF，若AC=，BC=9，则DF等于（　 　）

    A. B. C. 4 D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：

    若A，B，C为数轴上三点且点C在A，B之间，若点C到A的距离是点C到B的距离的3倍，我们就称点C是（A，B）的好点．

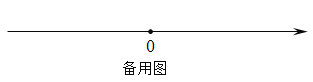
    例如，如图1，点A表示的数为－2，点B表示的数为2．表示1的点C到A的距离是3，到B的距离是1，那么点C是（A，B）的好点；又如，表示－1的点D到A的距离是1，到B的距离是3，那么点D就不是（A，B）的好点，但点D是（B，A）的好点．

    知识运用：

    （1）若M、N为数轴上两点，点M所表示的数为－6，点N所表示的数为2．

    数 所表示的点是（M，N）的好点；

    数 所表示的点是（N，M）的好点；

    （2）若点A表示的数为a，点B表示的数为b，点B在点A的右边，且点B在A， C之间，点B是（C，A）的好点，求点C所表示的数（用含a、b的代数式表示）；

    （3）若A、B为数轴上两点，点A所表示的数为－33，点B所表示的数为27，现有一只电子蚂蚁P从点A出发，以每秒6个单位的速度向右运动，运动时间为t秒．如果P，A，B中恰有一个点为其余两点的好点，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，方格图中每个小正方形的边长为1，点A、B、C都是格点．

    （1）画出△ABC关于直线MN对称的△A1B1C1；

    （2）直接写出AA1的长度；

    （3）如图2，A、C是直线MN同侧固定的点，D是直线MN上的一个动点，在直线MN上画出点D，使AD+DC最小．（保留作图痕迹）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

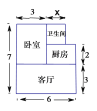
    【题目】某人准备购买一套小户型住房，他去某楼盘了解情况得知，该户型单价是元/，总面积如图所示（单位：米，卫生间的宽未定，设宽为米），售房部为他提供了以下两种优惠方案： 方案一：需购买全部总面积，但整套房按原销售总金额的9折出售；

    方案二：整套房的单价仍是12000元/，但不需要购买全部面积，其中，只对厨房面积进行了优惠，只算厨房的面积，其余房间面积不变．

    （1）求卫生间的面积；

    （2）请分别求出两种方案购买一套该户型商品房的总金额；

    （3）当1≤≤2，且为整数时，选哪种方案购买一套该户型商品房的总金额较少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CBF=∠CAB．

    （1）求证：直线BF是⊙O的切线；

    （2）若AB=5，sin∠CBF=,求BC和BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC，AB于点E，F．

    （1）试判断直线BC与⊙O的位置关系，并说明理由；

    （2）若BD=2，BF=2，求阴影部分的面积（结果保留π）．

    查看答案和解析>>

    同步练习册答案