
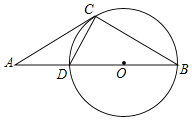
【题目】如图,点A是⊙O直径BD延长线上的一点,AC是⊙O的切线,C为切点.AD=CD,
(1)求证:AC=BC;
(2)若⊙O的半径为1,求△ABC的面积.
【答案】(1)证明见解析;(2)S△ABC=![]() .
.
【解析】
(1)连接OC,证得∠1=∠2,可得∠A=∠B,则结论得证;
(2)易证∠A=∠B=∠1=∠2=30°,即可求得AC的长,作CE⊥AB于点E,求得CE的长,利用三角形面积公式求解.
(1)证明:连接OC,
∵AC为切线,C为切点,
∴∠ACO=90°,
即∠DCO+∠2=90°,
又∵BD是直径,
∴∠BCD=90°,
即∠DCO+∠1=90°,
∴∠1=∠2,
∵AD=CD,OB=OC,
∴∠A=∠2,∠B=∠1,
∴∠A=∠B,
∴AC=BC;
(2)解:由题意可得△DCO是等腰三角形,
∵∠CDO=∠A+∠2,∠DOC=∠B+∠1,
∴∠CDO=∠DOC,即△DCO是等边三角形,
∴∠A=∠B=∠1=∠2=30°,CD=AD=1,
∴BC=![]() =
=![]() =
=![]() ,
,
在Rt△BCD中,作CE⊥AB于点E,
在Rt△BEC中,∠B=30°,
∴CE=![]() ,BE=
,BE=![]() ,
,
∴S△ABC=![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】有三张分别标有数字2,5,9的卡片,它们的背面都相同.现将它们背面朝上,从中任意抽出一张卡片,不放回,再从剩余的两张卡片里任意抽出一张.
(1)请用树状图或列表法表示出所有可能的结果.
(2)求两张卡片的数字之和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF。
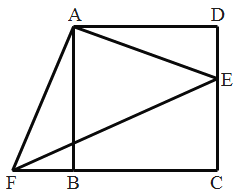
(1)求证:△ADE≌△ABF
(2)△ABF可以由△ADE绕旋转中心________点,按顺时针方向旋转________度得到;
(3)若BC=8,DE=3,求△AEF的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问锯几何?”用现代的数学语言表述是:“如图,CD为⊙O的直径,弦AB⊥CD垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意,CD长为( )
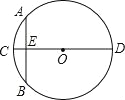
A.12寸 B.13寸 C.24寸 D.26寸
查看答案和解析>>
科目:初中数学 来源: 题型:
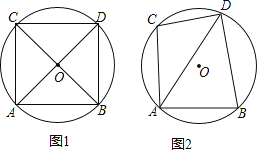
【题目】已知⊙O中,弦AB⊥AC,且AB=AC=6,点D在⊙O上,连接AD,BD,CD.
(1)如图1,若AD经过圆心O,求BD,CD的长;
(2)如图2,若∠BAD=2∠DAC,求BD,CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线S1与x轴交于点A(﹣3,0),B(1,0),将它向右平移2个单位得新抛物线S2,点M,N是抛物线S2上两点,且MN∥x轴,交抛物线S1于点C,已知MN=3MC,则点C的横坐标为( )
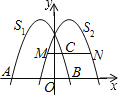
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(3, 2),点B的坐标为(3, 0). 作如下操作:①以点A为旋转中心,把△ABO顺时针旋转90°,得到△ACD;
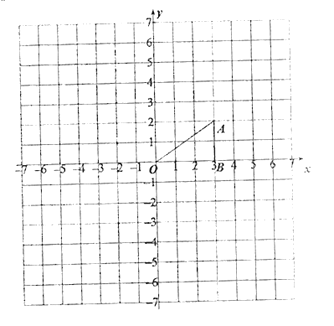
(1)在图中画出△ACD;
(2)①请直接写点B旋转到点C的路径长:____________;
②画出△ABO关于点O的中心对称图形△EOF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.
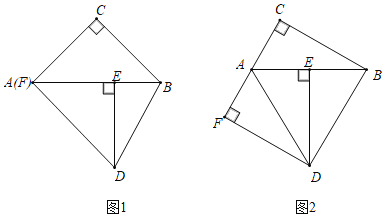
(1)如图1,若点F与点A重合,求证:AC=BC.
(2)如图2,若点F在线段CA的延长线上,∠DAF=∠DBA,请判断线段AF与BE的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com