
如图,等腰△ABC中,AB=BC,∠B=120o,M,N分别是AB,BC边上的中点.
(1)用尺规作图的方法,在AC上找一点P,使得MP+NP最短.
(不用写作法,保留作图痕迹)
(2)若AC边上的高为1,求MP+NP的最短长度.
 |
 (1)如图所示,点P即为所求.…………………2分
(1)如图所示,点P即为所求.…………………2分
(![]() 2)连接AM’,MP,BP……………………………3分
2)连接AM’,MP,BP……………………………3分
∵点M’和点M关于AC对称
∴MP=M’P, ∠MPA=∠M’PA
又∵PA=PA
 ∴△MPA≌△M’PA………………………………4分
∴△MPA≌△M’PA………………………………4分
∴∠BAC=∠M’AC,AM=AM’…………………….5分
又∵AB=BC
∴∠BAC=∠C
∴∠M’AC=∠C…………………………………….6分
又∵M,N分别为AB,BC边上的中点
∴AM=NC
即:AM’=NC…………………………………………7分
又∵∠APM’=∠CPN
∴△APM’≌△CPN……………………………![]() ……..8分
……..8分
∴AP=PC
∴BP为AC边上的高…………………………………9分
又∵在Rt△ABP中,∠BAP=30![]() o
o
∴BP=![]() AB=MB…………………………………….10分
AB=MB…………………………………….10分
又∵∠ABP=60o.
∴△BMP为等边三角形…………………………………11分
∴MP=BP=1………………………………………………12分
同理:NP=1……………………………………………..13分
∴MP+NP的最短长度为2.…………………………14分


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
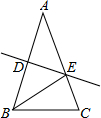 如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )| A、80° | B、70° | C、60° | D、50° |
查看答案和解析>>
科目:初中数学 来源: 题型:
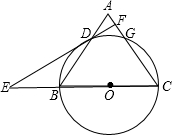 如图,等腰△ABC中,AC=BC=10,AB=12,以BC为直径作⊙0交AB于D,交AC于G,DF⊥AC,垂足为F,交CB的延长线于点E,则sinE=
如图,等腰△ABC中,AC=BC=10,AB=12,以BC为直径作⊙0交AB于D,交AC于G,DF⊥AC,垂足为F,交CB的延长线于点E,则sinE=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com