
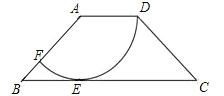
【题目】如图,在四边形ABCD中,AD∥BC,AD=2,AB=![]() ,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
(1)求∠ABE的大小及![]() 的长度;
的长度;
(2)在BE的延长线上取一点G,使得![]() 上的一个动点P到点G的最短距离为
上的一个动点P到点G的最短距离为![]() ,求BG的长.
,求BG的长.
【答案】(1)45°,![]() ;(2)4.
;(2)4.
【解析】
试题分析:(1)连接AE,如图1,根据圆的切线的性质可得AE⊥BC,解Rt△AEB可求出∠ABE,进而得到∠DAB,然后运用圆弧长公式就可求出![]() 的长度;
的长度;
(2)如图2,根据两点之间线段最短可得:当A、P、G三点共线时PG最短,此时AG=AP+PG=![]() =AB,根据等腰三角形的性质可得BE=EG,只需运用勾股定理求出BE,就可求出BG的长.
=AB,根据等腰三角形的性质可得BE=EG,只需运用勾股定理求出BE,就可求出BG的长.
试题解析:(1)连接AE,如图1,∵AD为半径的圆与BC相切于点E,∴AE⊥BC,AE=AD=2.
在Rt△AEB中,sin∠ABE=![]() =
=![]() =
=![]() ,∴∠ABE=45°.∵AD∥BC,∴∠DAB+∠ABE=180°,∴∠DAB=135°,∴
,∴∠ABE=45°.∵AD∥BC,∴∠DAB+∠ABE=180°,∴∠DAB=135°,∴![]() 的长度为
的长度为![]() =
=![]() ;
;
(2)如图2,根据两点之间线段最短可得:当A、P、G三点共线时PG最短,此时AG=AP+PG=![]() =
=![]() ,∴AG=AB.∵AE⊥BG,∴BE=EG.∵BE=
,∴AG=AB.∵AE⊥BG,∴BE=EG.∵BE=![]() =
=![]() =2,∴EG=2,∴BG=4.
=2,∴EG=2,∴BG=4.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商城某专卖店销售每件成本为40元的商品,从销售情况中随机抽取一些情况制成统计表如下:(假设当天定的售价是不变的,且每天销售情况均服从这种规律)
每件销售价(元) | 50 | 60 | 70 | 75 | 80 | 85 | …… |
每天售出件数 | 300 | 240 | 180 | 150 | 120 | 90 | …… |
(1)观察这些数据,找出每天售出件数y与每件售价x(元)之间的函数关系,并写出该函数关系式;
(2)该店原有两名营业员,但当每天售出量超过168件时,则必须增派一名营业员才能保证营业,设营业员每人每天工资为40元,求每件产品定价多少元,才能使纯利润最大(纯利润指的是收入总价款扣除成本及营业员工资后的余额,其他开支不计).
查看答案和解析>>
科目:初中数学 来源: 题型:
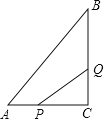
【题目】如图,在△ABC中,∠C=90°,AC=6cm,BC=8m,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动,当其中一点到达终点时,另一点也随之停止运动.
(1)如果点P,Q同时出发,经过几秒钟时△PCQ的面积为8cm2?
(2)如果点P,Q同时出发,经过几秒钟时以P、C、Q为顶点的三角形与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6 000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
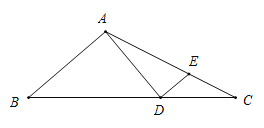
【题目】如图,在![]() ABC中,点D为BC边上的一点,且AD=AB=5, AD⊥AB于点A,过点D作DE⊥AD,DE交AC于点E,若DE=2,则
ABC中,点D为BC边上的一点,且AD=AB=5, AD⊥AB于点A,过点D作DE⊥AD,DE交AC于点E,若DE=2,则![]() ADC的面积为( )
ADC的面积为( )
A.![]() B.4C.
B.4C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为(4,0),点B为y轴上的一动点,将线段AB绕点B顺时针旋转90°得线段BC,若点C恰好落在反比例函数y=![]() 的图象上,则点B的坐标为_____.
的图象上,则点B的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com