
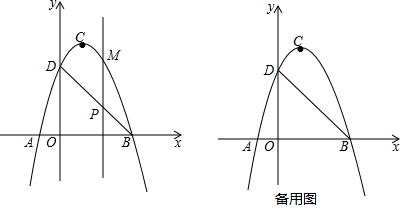
分析 (1)可设抛物线解析式为顶点式,由B点坐标可求得抛物线的解析式,则可求得D点坐标,利用待定系数法可求得直线BD解析式;
(2)设出P点坐标,从而可表示出PM的长度,利用二次函数的性质可求得其最大值;
(3)过Q作QG∥y轴,交BD于点G,过Q和QH⊥BD于H,可设出Q点坐标,表示出QG的长度,由条件可证得△DHG为等腰直角三角形,则可得到关于Q点坐标的方程,可求得Q点坐标.
解答 解:
(1)∵抛物线的顶点C的坐标为(1,4),
∴可设抛物线解析式为y=a(x-1)2+4,
∵点B(3,0)在该抛物线的图象上,
∴0=a(3-1)2+4,解得a=-1,
∴抛物线解析式为y=-(x-1)2+4,即y=-x2+2x+3,
∵点D在y轴上,令x=0可得y=3,
∴D点坐标为(0,3),
∴可设直线BD解析式为y=kx+3,
把B点坐标代入可得3k+3=0,解得k=-1,
∴直线BD解析式为y=-x+3;
(2)设P点横坐标为m(m>0),则P(m,-m+3),M(m,-m2+2m+3),
∴PM=-m2+2m+3-(-m+3)=-m2+3m=-(m-$\frac{3}{2}$)2+$\frac{9}{4}$,
∴当m=$\frac{3}{2}$时,PM有最大值$\frac{9}{4}$;
(3)如图,过Q作QG∥y轴交BD于点G,交x轴于点E,作QH⊥BD于H,
设Q(x,-x2+2x+3),则G(x,-x+3),
∴QG=|-x2+2x+3-(-x+3)|=|-x2+3x|,
∵△BOD是等腰直角三角形,
∴∠DBO=45°,
∴∠HGQ=∠BGE=45°,
当△BDQ中BD边上的高为2$\sqrt{2}$时,即QH=HG=2$\sqrt{2}$,
∴QG=$\sqrt{2}$×2$\sqrt{2}$=4,
∴|-x2+3x|=4,
当-x2+3x=4时,△=9-16<0,方程无实数根,
当-x2+3x=-4时,解得x=-1或x=4,
∴Q(-1,0)或(4,-5),
综上可知存在满足条件的点Q,其坐标为(-1,0)或(4,-5).
点评 本题为二次函数的综合应用,涉及待定系数法、二次函数的性质、等腰直角三角形的性质及方程思想等知识.在(1)中主要是待定系数法的考查,注意抛物线顶点式的应用,在(2)中用P点坐标表示出PM的长是解题的关键,在(3)中构造等腰直角三角形求得QG的长是解题的关键.本题考查知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
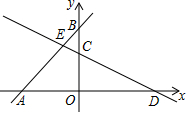 如图,直线y=mx+3与x轴、y轴交于点A、点B,直线CD与x轴交于点D,与y轴交于点C(0,2),与直线AB交于点E,点E的坐标为(-$\frac{2}{3}$,$\frac{7}{3}$).
如图,直线y=mx+3与x轴、y轴交于点A、点B,直线CD与x轴交于点D,与y轴交于点C(0,2),与直线AB交于点E,点E的坐标为(-$\frac{2}{3}$,$\frac{7}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
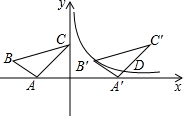 如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2)将△ABC沿x轴向右平移7个单位得到△A′B′C′,点B′恰好在反比例函数y=$\frac{k}{x}$的图象上,且反比例函数图象与A′C′相交于点D.
如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(-5,2)将△ABC沿x轴向右平移7个单位得到△A′B′C′,点B′恰好在反比例函数y=$\frac{k}{x}$的图象上,且反比例函数图象与A′C′相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com