
【题目】在平面直角坐标系中,直线y=﹣![]() x+6分别与x轴、y轴交于点A,B.当点P在线段AB(点P不与A,B重合)上运动时,在坐标系内存在一点N,使得以O,B,P,N为顶点的四边形为菱形.请直接写出N点坐标_____.
x+6分别与x轴、y轴交于点A,B.当点P在线段AB(点P不与A,B重合)上运动时,在坐标系内存在一点N,使得以O,B,P,N为顶点的四边形为菱形.请直接写出N点坐标_____.
【答案】(﹣4,3),(![]() ,
,![]() ),(
),(![]() ,﹣
,﹣![]() ).
).
【解析】
直接考虑以O,B,P,N为顶点的菱形中的数量关系比较复杂,不妨根据菱形的性质,它的一半为等腰三角形,则讨论三边有任意两边相等,分三种情况: BP=OP, OP=OB, BP=OB,再根据坐标系中任意两点间的距离公式列出等式解答即可.
解:∵直线y=﹣![]() x+6分别与x轴、y轴交于点A,B,
x+6分别与x轴、y轴交于点A,B,
∴A(8,0),B(0,6).
分三种情况:
①如图所示,以OB为菱形OPBN的对角线,点P与点N关于OB对称,
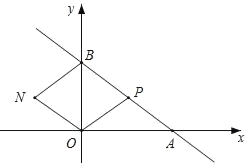
由BP=OP可得,∠PBO=∠POB,
根据∠PBO+∠PAO=∠POB+∠POA=90°,可得∠POA=∠PAO,
∴PO=PA,
∴P是AB的中点,即P(4,3),
∴N(﹣4,3);
②如图所示,以PB为菱形OPBN的对角线,设P(n,﹣![]() n+6),
n+6),

∵四边形OPNB为菱形,B(0,6),
∴OP=OB=6=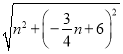 ,
,
解得:n=![]() 或n=0(舍去),
或n=0(舍去),
∴点P(![]() ,
,![]() ),
),
∴点N(![]() ,
,![]() ),即N(
),即N(![]() ,
,![]() );
);
③如图所示,以OP为菱形BPNO的对角线,设P(m,﹣![]() m+6)
m+6)
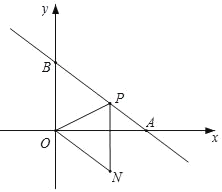
∵四边形ONPB为菱形, B(0,6),
∴BP=OB=6= ,
,
解得m=![]() ,
,
∴P(![]() ,
,![]() ),
),
∴N(![]() ,
,![]() ),即N(
),即N(![]() ,﹣
,﹣![]() ),
),
综上所述,N点坐标为(﹣4,3),(![]() ,
,![]() ),(
),(![]() ,﹣
,﹣![]() ).
).
故答案为:(﹣4,3),(![]() ,
,![]() ),(
),(![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
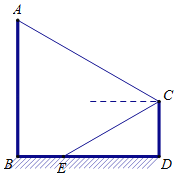
【题目】某游乐场一转角滑梯如图所示,滑梯立柱AB、CD均垂直于地面,点E在水平地面上BD上,在C点测得点A的仰角为30°,斜面EC的坡度为1:![]() ,测得B、E间距离为10米,立柱AB高30米,求立柱CD的高(结果保留根号).
,测得B、E间距离为10米,立柱AB高30米,求立柱CD的高(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() 两点横坐标为
两点横坐标为![]() 和
和![]() ,
,![]() 点纵坐标为
点纵坐标为![]() .
.

![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 动点
动点![]() 在第四象限且在抛物线上,当
在第四象限且在抛物线上,当![]() 面积最大时,求
面积最大时,求![]() 点坐标,并求
点坐标,并求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字﹣1,0,1,2的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗均匀.
(1)随机抽取一张卡片,求抽到数字“﹣1”的概率;
(2)随机抽取一张卡片,然后不放回,再随机抽取一张卡片,请用列表或画树状图的方法求出第一次抽到数字“2”且第二次抽到数字“0”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由两个可以自由转动的转盘、每个转盘被分成如图所示的几个扇形、游戏者同时转动两个转盘,如果一个转盘转出了红色,另一转盘转出了蓝色,游戏者就配成了紫色下列说法正确的是( )
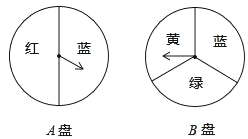
A. 两个转盘转出蓝色的概率一样大
B. 如果A转盘转出了蓝色,那么B转盘转出蓝色的可能性变小了
C. 先转动A 转盘再转动B 转盘和同时转动两个转盘,游戏者配成紫色的概率不同
D. 游戏者配成紫色的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的操作规则
第一次操作:对任意相邻的两个数,都用左边的数减去右边的数,所得的差写在这两个数之间,得到一组依次排列的新数串;第二次操作:对上一次操作得到的新数串,仍按照第一次操作进行,又得到一组依次排列的新数串;……这样依次操作下去
(1)对依次排列的3个数:﹣2,3,6,按上面的规则进行操作,
①齐第一次操作后得到的新数串:﹣2, ,3, ,6此次增加的新数之和为 ;
②出第二次操作后得到的新数中,并求第二次操作后再次增加的新数之和;
(2)对依次排列的3个数:1,3,﹣![]() ,按上述规则操作,直接写出第三次操作后再次增加的新数之和是 .
,按上述规则操作,直接写出第三次操作后再次增加的新数之和是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
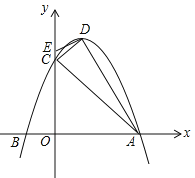
【题目】已知,抛物线![]() (a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE=
(a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE=![]() .
.
(1)求抛物线的解析式及顶点D的坐标;
(2)求证:直线DE是△ACD外接圆的切线;
(3)在直线AC上方的抛物线上找一点P,使![]() ,求点P的坐标;
,求点P的坐标;
(4)在坐标轴上找一点M,使以点B、C、M为顶点的三角形与△ACD相似,直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汛期到来,山洪暴发.下表记录了某水库![]() 内水位的变化情况,其中
内水位的变化情况,其中![]() 表示时间(单位:
表示时间(单位:![]() ),
),![]() 表示水位高度(单位:
表示水位高度(单位:![]() ),当
),当![]() 时,达到警戒水位,开始开闸放水.
时,达到警戒水位,开始开闸放水.
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 14 | 15 | 16 | 17 | 18 | 14.4 | 12 | 10.3 | 9 | 8 | 7.2 |

(1)在给出的平面直角坐标系中,根据表格中的数据描出相应的点.
(2)请分别求出开闸放水前和放水后最符合表中数据的函数解析式.
(3)据估计,开闸放水后,水位的这种变化规律还会持续一段时间,预测何时水位达到![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com