
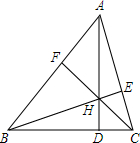
 如图,已知锐角△ABC的三条高AD、BE、CF交于点H,BC=a,AC=b,AB=c.求证:AH•AD+BH•BE+CH•CF=$\frac{1}{2}$(a2+b2+c2).
如图,已知锐角△ABC的三条高AD、BE、CF交于点H,BC=a,AC=b,AB=c.求证:AH•AD+BH•BE+CH•CF=$\frac{1}{2}$(a2+b2+c2). 分析 因H为△ABC垂心,故H、D、C、E四点共圆,根据切割线定理即可求解.
解答 证明:∵锐角△ABC的三条高AD、BE、CF交于点H,
∴∠CEH+∠CDH=180°,
∴H、D、C、E四点共圆,
∴AH•AD=AC•AE=AC•AB•cos∠BAE=$\frac{1}{2}$(b2+c2-a2),
同理可得:BH•BE=$\frac{1}{2}$(a2+c2-b2),CH•CF=$\frac{1}{2}$(a2+b2-c2),
故AH•AD+BH•BE+CH•CF=$\frac{1}{2}$(a2+b2+c2).
点评 本题主要考查了切割线定理以及三角形边角关系,理解H、D、C、E四点共圆是解决本题的关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:选择题
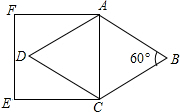 如图,在菱形ABCD中,∠B=60°,若正方形ACEF的周长为a,菱形ABCD的周长为b,则a与b的大小关系为( )
如图,在菱形ABCD中,∠B=60°,若正方形ACEF的周长为a,菱形ABCD的周长为b,则a与b的大小关系为( )| A. | a>b | B. | a<b | C. | a=b | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC的三个顶点郡在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针方向旋转到△A′BC′的位置,且点A′,C′仍落在格点上,则线段A′B的长是$\sqrt{13}$.
如图,△ABC的三个顶点郡在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针方向旋转到△A′BC′的位置,且点A′,C′仍落在格点上,则线段A′B的长是$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com