
【题目】在平面直角坐标中,等腰Rt△ABC中,AB=AC,∠CAB=90°,A(0,a),B(b,0).

(1)如图1,若![]() +(a-2)2=0,求△ABO的面积;
+(a-2)2=0,求△ABO的面积;
(2)如图2,AC与x轴交于D点,BC与y轴交于E点,连接DE,AD=CD,求证:∠ADB=∠CDE;
(3)如图3,在(1)的条件下,若以P(0,-6)为直角顶点,PC为腰作等腰Rt△PQC,连接BQ,求证:AP∥BQ.
【答案】(1)△ABO的面积=4;(2)证明见解析;(3)证明见解析.
【解析】
(1)根据绝对值和偶次方的非负性求出a,b,根据三角形的面积公式计算;
(2)作AF平分∠BAC交BD于F点,分别证明△ACE≌△BAF,△CED≌△AFD,根据全等三角形的性质证明;
(3)过C点作CM⊥y轴于M点,过D点作DN⊥y轴于N点,证明△ACM≌△BAO,根据全等三角形的性质得到CM=AO=2,AM=BO=4,证明四边形ONQB为平行四边形,得到答案.
解:(1)∵![]() +(a-2)2=0,
+(a-2)2=0,
∴2a-b=0,a-2=0,
解得,a=2,b=4,
∴A(0,2),B(4,0),
∴OA=2,OB=4,
∴△ABO的面积=![]() ×2×4=4;
×2×4=4;

(2)作AF平分∠BAC交BD于F点,
∵AB=AC,∠CAB=90°,
∴∠C=∠ABC=∠DAF=∠BAF=45°,
∵∠CAE+∠BAO=∠ABF+∠BAO=90°,
∴∠CAE=∠ABF,
在△ACE和△BAF中,
 ,
,
∴△ACE≌△BAF(ASA),
∴CE=AF,
在△CED和△AFD中,
 ,
,
∴△CED≌△AFD(SAS)
∴∠CDE=∠ADB;
(3)过C点作CM⊥y轴于M点,过D点作DN⊥y轴于N点,
则∠AMC=∠BOA=90°,
∵∠CAM+∠BAO=∠ABO+∠BAO=90°,
∴∠CAM=∠ABO,
在△ACM和△BAO中,
 ,
,
∴△ACM≌△BAO(AAS),
∴CM=AO=2,AM=BO=4,
∵A(0,2),P(0,-6),
∴AP=8,
∴PM=AP-AM=4,
在△PCM和△QPN中,
 ,
,
△PCM≌△QPN(AAS),
∴NQ=PM=4,
∴四边形ONQB为平行四边形,
∴AP∥BQ.



科目:初中数学 来源: 题型:
【题目】某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,其中购进电冰箱x台(33≤x≤40),那么该商店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
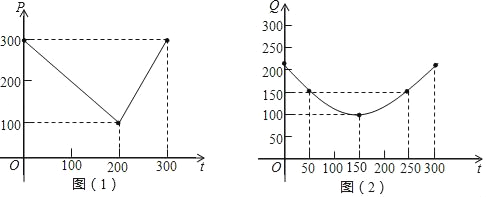
【题目】(7分)某蔬菜基地种植西红柿,由历年市场行情得知,从2月1日起的300天内,西红柿市场售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段Q=![]() (t﹣150)2+100 (0≤t≤300)表示,(注:市场售价和种植成本的单位:元/100kg,时间单位:天)
(t﹣150)2+100 (0≤t≤300)表示,(注:市场售价和种植成本的单位:元/100kg,时间单位:天)
(1)写出图(1)表示的市场售价P与时间t的函数关系式;
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是![]() 的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF, BE=7.5, CF=6,则EF=( ).
的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF, BE=7.5, CF=6,则EF=( ).

A.2.5B.2C.1.5D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的顶点坐标分别为A(2,3)、B (1,1)、C(2,1)
的顶点坐标分别为A(2,3)、B (1,1)、C(2,1)

(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ,并写出点
,并写出点![]() 的坐标为_________
的坐标为_________
(2)将![]() 向左平移4个单位长度得到
向左平移4个单位长度得到![]() ,直接写出点
,直接写出点![]() 的坐标为_________
的坐标为_________
(3)直接写出点B关于直线n(直线n上各点的纵坐标都为-1)对称点B'的坐标为________
(4)在![]() 轴上找一点P,使PA+PB的值最小,标出P点的位置(保留画图痕迹)
轴上找一点P,使PA+PB的值最小,标出P点的位置(保留画图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)
如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(![]() )
)![]() ,正六边形的边长为(
,正六边形的边长为(![]() )cm(其中
)cm(其中![]() ),求这两段铁丝的总长
),求这两段铁丝的总长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两组算式,解答问题:
第一组:![]() =2,
=2,![]() =2,
=2,![]() 、
、![]() ,
,![]() =0
=0
第二组:![]() =2,
=2,![]() =3,
=3,![]() =9,
=9,![]() =16,
=16,![]() =0
=0
(1)由第一组可得结论:对于任意实数a,![]() =_____.
=_____.
(2)由第二组可得结论:当a≥0时,![]() =_____.
=_____.
(3)利用(1)和(2)的结论计算:![]() =_____,
=_____,![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒?四边形PBCQ的面积为33cm2;
(2)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com