我市“上品”房地产开发公司于2010年5月份完工一商品房小区,6月初开始销售,其中6月的销售单价为0.7万元/m2,7月的销售单价为0.72万元/m2,且每月销售价格y1(单位:万元/m2)与月份x(6≤x≤11,x为整数)之间满足一次函数关系:每月的销售面积为y2(单位:m2),其中y2=-2000x+26000(6≤x≤11,x为整数).
(1)求y1与月份x的函数关系式;
(2)6~11月中,哪一个月的销售额最高?最高销售额为多少万元?
(3)2010年11月时,因会受到即将实行的“国八条”和房产税政策的影响,该公司销售部预计12月份的销售面积会在11月销售面积基础上减少20a%,于是决定将12月份的销售价格在11月的基础上增加a%,该计划顺利完成.为了尽快收回资金,2011年1月公司进行降价促销,该月销售额为(1500+600a)万元.这样12月、1月的销售额共为4618.4万元,请根据以上条件求出a的值为多少?
解:(1)设y
1=kx+b(k≠0),
由题意
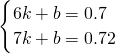
解得:

.
(2)设第x个月的销售额为W万元,
则W=y
1y
2=(0.02x+0.58)(-2000x+26000)
=-40x
2-640x+15080,
∴对称轴为直线x=-

=-

=-8,
∵当6≤x≤11是W随x的增大而减小,
∴当x=6时,
W
max=-40×6
2-640×6+15080=9800
∴6月份的销售额最大为9800万元.
(3)11月的销售面积为:-2000×11+26000=4000(m
2)
11月份的销售价格为:0.02×11+0.58=0.8(万元/m
2)
由题意得:4000(1-20a%)×0.8(1+a%)+1500+600a=4618.4,
化简得:4a
2+5a-51=0,解得:

(舍)
∴a=3.
分析:(1)设y
1=kx+b,运用待定系数法求解即可.
(2)根据题意表示出月销售额W的表达式,然后根据二次函数的最值可求得答案.
(3)先求出11月的销售面积为及11月份的销售价格,然后根据题意可得出关于a的一元二次方程,解出即可得出答案.
点评:本题考查了待定系数法求函数解析式及二次函数的应用,综合性较强,难度较大,解答此类题目是要仔细审题,建立数学模型,运用所学的知识解答实际问题.

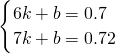
 .
. =-
=- =-8,
=-8, (舍)
(舍)

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案 (k≠0)的图象上.
(k≠0)的图象上.