
”¾ĢāÄæ”抔Ć÷“Ó¼Ņ³ö·¢ŃŲ±õ½Ā·µ½ĶāĢ²¹«Ō°Ķ½²½¶ĶĮ¶£¬µ½ĶāĢ²¹«Ō°ŗóĮ¢¼“ŃŲŌĀ··µ»Ų£¬Š”Ć÷ĄėæŖ¼ŅµÄĀ·³Ģs£Øµ„Ī»£ŗĒ§Ć×£©Óė×ß²½Ź±¼ät£Øµ„Ī»£ŗŠ”Ź±£©Ö®¼äµÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£¬ĘäÖŠ“Ó¼Ņµ½ĶāĢ²¹«Ō°µÄĘ½¾łĖŁ¶ČŹĒ4Ē§Ć×/Ź±£¬øł¾ŻĶ¼ŠĪĢį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ĒóĶ¼ÖŠµÄaÖµ£»
£Ø2£©ČōŌŚ¾ąĄėŠ”Ć÷¼Ņ5Ē§Ćד¦ÓŠŅ»øöµŲµćC£¬Š”Ć÷“ÓµŚŅ»²ć¾¹żµćCµ½µŚ¶ž²ć¾¹żµćC£¬ĖłÓĆŹ±¼äĪŖ1.75Š”Ź±£¬ĒóŠ”Ć÷·µ»Ų¹ż³ĢÖŠ£¬sÓėtµÄŗÆŹż½āĪöŹ½£¬²»±ŲŠ“³ö×Ō±äĮæµÄȔֵ·¶Ī§£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬ĒóŠ”Ć÷“Ó³ö·¢µ½»Ųµ½¼ŅĖłÓƵď±¼ä£®

”¾“š°ø”æ£Ø1£©8£»£Ø2£©s=©3t+14£»£Ø3£©Š”Ć÷“Ó³ö·¢µ½»Ųµ½¼ŅĖłÓƵď±¼äŹĒ![]() Š”Ź±£®
Š”Ź±£®
”¾½āĪö”æ·ÖĪö: £Ø1£©øł¾ŻĀ·³Ģ=ĖŁ¶Č”ĮŹ±¼ä¼“æÉĒó³öaÖµ£»
£Ø2£©øł¾ŻĖŁ¶Č=Ā·³Ģ”ĀŹ±¼äĒó³ö“ĖČĖ·µ»ŲŹ±µÄĖŁ¶Č£¬ŌŁøł¾ŻĀ·³Ģ=8-·µ»ŲŹ±µÄĖŁ¶Č”ĮŹ±¼ä¼“æÉµĆ³öABĖłŌŚÖ±ĻßµÄŗÆŹż½āĪöŹ½£»
£Ø3£©Įī£Ø2£©ÖŠµÄŗÆŹż¹ŲĻµŹ½ÖŠs=0£¬Ēó³ötÖµ¼“æÉ£®
Ļź½ā:
£Ø1£©ÓÉĢāŅāæÉµĆ£¬
a=2”Į4=8£¬
¼“aµÄÖµŹĒ8£»
£Ø2£©ÓÉĢāŅāæÉµĆ£¬
Š”Ć÷“Ó¼Ņµ½¹«Ō°µÄ¹ż³ĢÖŠ£¬Cµćµ½AµćÓƵď±¼äĪŖ£ŗ£Ø8©5£©”Ā4=0.75Š”Ź±£¬
Š”Ć÷“Ó¹«Ō°µ½¼ŅµÄ¹ż³ĢÖŠ£¬Aµćµ½CµćÓƵď±¼äĪŖ1.75©0.75=1Š”Ź±£¬ĖŁ¶ČĪŖ£ŗ£Ø8©5£©”Ā1=3Ē§Ć×/Ź±£¬
¹ŹŠ”Ć÷“Ó¹«Ō°µ½¼ŅÓƵď±¼äĪŖ£ŗ8”Ā3=![]() Š”Ź±£¬
Š”Ź±£¬
”ąµćA£Ø2£¬8£©£¬µćB£Ø![]() £¬0£©
£¬0£©
É芔Ć÷·µ»Ų¹ż³ĢÖŠ£¬sÓėtµÄŗÆŹż½āĪöŹ½ŹĒs=kt+b£¬
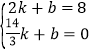 £¬µĆ
£¬µĆ![]()
¼“Š”Ć÷·µ»Ų¹ż³ĢÖŠ£¬sÓėtµÄŗÆŹż½āĪöŹ½ŹĒs=©3t+14£»
£Ø3£©µ±s=0Ź±£¬©3t+14=0£¬µĆt=![]() £¬
£¬
“š£ŗŠ”Ć÷“Ó³ö·¢µ½»Ųµ½¼ŅĖłÓƵď±¼äŹĒ![]() Š”Ź±£®
Š”Ź±£®
µć¾¦: ±¾Ģāæ¼²éŅ»“ĪŗÆŹżµÄÓ¦ÓĆ£¬½ā“š±¾ĢāµÄ¹Ų¼üŹĒĆ÷Č·ĢāŅā£¬Ēó³öĻąÓ¦µÄŗÆŹż½āĪöŹ½£¬ĄūÓĆŗÆŹżµÄĖ¼ĻėŗĶŹżŠĪ½įŗĻµÄĖ¼Ļė½ā“š£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻß![]() Óė
Óė![]() Öį½»ÓŚA£¬BĮ½µć(µćBŌŚµćAµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµćC£¬¶„µćĪŖD£¬Ęä¶Ō³ĘÖįÓė
Öį½»ÓŚA£¬BĮ½µć(µćBŌŚµćAµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµćC£¬¶„µćĪŖD£¬Ęä¶Ō³ĘÖįÓė![]() Öį½»ÓŚµćE£¬ĮŖ½ÓAD£¬OD£®
Öį½»ÓŚµćE£¬ĮŖ½ÓAD£¬OD£®
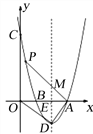
£Ø1£©Ē󶄵ćDµÄ×ų±ź£ØÓĆŗ¬![]() µÄŹ½×Ó±ķŹ¾£©£»
µÄŹ½×Ó±ķŹ¾£©£»
£Ø2£©ČōOD”ĶAD£¬ĒóøĆÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Éč¶ÆµćPŌŚ¶Ō³ĘÖį×ó²ąøĆÅ×ĪļĻßÉĻ£¬PAÓė¶Ō³ĘÖį½»ÓŚµćM£¬Čō”÷AMEÓė”÷OADĻąĖĘ£¬ĒóµćPµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ³ö×ā³µĖ¾»śŠ”Ąī¹śĒģ³¤¼ŁĘŚ¼äµÄijĢģĻĀĪēµÄÓŖŌĖČ«ŹĒŌŚÄĻ±±×ßĻņµÄ³ĒĒųŹŠŠÄĀ·ÉĻ½ųŠŠµÄ£¬Čē¹ū¹ę¶ØĻņÄĻŠŠŹ»ĪŖÕż£¬ĖūÕāĢģĻĀĪēŠŠ³µµÄĄļ³Ģ£Øµ„Ī»£ŗĒ§Ć×£©ČēĻĀ£ŗ
+8£¬©6£¬©5£¬+10£¬©5£¬+3£¬©2£¬+6£¬+2£¬©5
£Ø1£©Š”ĄīĻĀĪē³ö·¢µŲ¼ĒĪŖ0£¬Ėū½«×īŗóŅ»Ćū³ĖæĶĖĶµÖÄæµÄµŲŹ±£¬Š”Ąī¾ąĻĀĪē³ö·¢µŲÓŠ¶ąŌ¶£æ
£Ø2£©Čē¹ūĘū³µŗÄÓĶĮæĪŖ0.4Éż/Ē§Ć×£¬ÓĶ¼ŪĆæÉż5.80ŌŖ£¬ÄĒĆ“ÕāĢģĻĀĪēĘū³µ¹²Šč»Ø·ŃÓĶ¼ŪĪŖ¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻC=90”ć£¬”ĻA=30”ć£¬AC=4£¬MŹĒAB±ßÉĻŅ»¶Æµć£¬NŹĒAC±ßÉĻµÄŅ»¶Æµć£¬ŌņMN+MCµÄ×īŠ”ÖµĪŖ_____£®
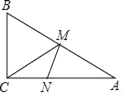
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijũæĘĖł¶Ō¼×”¢ŅŅĮ½ÖÖŠ”Āóø÷Ń”ÓĆ10æéĆ껿ĻąĶ¬µÄŹŌŃéĢļ½ųŠŠÖÖÖ²ŹŌŃ飬ĖüĆĒµÄĘ½¾łÄ¶²śĮæ·Ö±šŹĒ![]() =610Ē§æĖ£¬
=610Ē§æĖ£¬![]() =608Ē§æĖ£¬Ä¶²śĮæµÄ·½²ī·Ö±šŹĒ
=608Ē§æĖ£¬Ä¶²śĮæµÄ·½²ī·Ö±šŹĒ![]() ="29." 6£¬
="29." 6£¬![]() ="2." 7. Ōņ¹ŲÓŚĮ½ÖÖŠ”ĀóĶĘ¹ćÖÖÖ²µÄŗĻĄķ¾ö²ßŹĒ £Ø £©
="2." 7. Ōņ¹ŲÓŚĮ½ÖÖŠ”ĀóĶĘ¹ćÖÖÖ²µÄŗĻĄķ¾ö²ßŹĒ £Ø £©
A. ¼×µÄĘ½¾łÄ¶²śĮæ½Ļøߣ¬Ó¦ĶĘ¹ć¼×
B. ¼×”¢ŅŅµÄĘ½¾łÄ¶²śĮæĻą²ī²»¶ą£¬¾łæÉĶĘ¹ć
C. ¼×µÄĘ½¾łÄ¶²śĮæ½Ļøߣ¬ĒŅĶ²śĮæ±Č½ĻĪČ¶Ø£¬Ó¦ĶĘ¹ć¼×
D. ¼×”¢ŅŅµÄĘ½¾łÄ¶²śĮæĻą²ī²»¶ą£¬µ«ŅŅµÄĶ²śĮæ±Č½ĻĪČ¶Ø£¬Ó¦ĶĘ¹ćŅŅ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½ü¼øÄź£¬Č«Éē»į¶ŌæÕĘųĪŪČ¾ĪŹĢāŌ½Ą“Ō½ÖŲŹÓ£¬æÕĘų¾»»ÆĘ÷µÄĻśĮæŅ²ŌŚÖšÄźŌö¼Ó£®Ä³ÉĢ³”“Ó³§¼Ņ¹ŗ½ųĮĖA£¬BĮ½ÖÖŠĶŗŵÄæÕĘų¾»»ÆĘ÷£¬Į½ÖÖ¾»»ÆĘ÷µÄĻśŹŪĻą¹ŲŠÅĻ¢¼ūĻĀ±ķ£ŗ
AŠĶĻśŹŪŹżĮæ£ØĢØ£© | BŠĶĻśŹŪŹżĮæ£ØĢØ£© | ×ÜĄūČó£ØŌŖ£© |
5 | 10 | 2 000 |
10 | 5 | 2 500 |
£Ø1£©ĆæĢØAŠĶæÕĘų¾»»ÆĘ÷ŗĶBŠĶæÕĘų¾»»ÆĘ÷µÄĻśŹŪĄūČó·Ö±šŹĒ¶ąÉŁ£æ
£Ø2£©øĆ¹«Ė¾¼Ę»®Ņ»“Ī¹ŗ½ųĮ½ÖÖŠĶŗŵÄæÕĘų¾»»ÆĘ÷¹²100ĢØ£¬ĘäÖŠBŠĶæÕĘų¾»»ÆĘ÷µÄ½ų»õĮæ²»ÉŁÓŚAŠĶæÕĘų¾»»ÆĘ÷µÄ2±¶£¬ĪŖŹ¹øĆ¹«Ė¾ĻśŹŪĶźÕā100ĢØæÕĘų¾»»ÆĘ÷ŗóµÄ×ÜĄūČó×ī“ó£¬ĒėÄćÉč¼ĘĻąÓ¦µÄ½ų»õ·½°ø£»
£Ø3£©ŅŃÖŖAŠĶæÕĘų¾»»ÆĘ÷µÄ¾»»ÆÄÜĮ¦ĪŖ300 m3/Š”Ź±£¬BŠĶæÕĘų¾»»ÆĘ÷µÄ¾»»ÆÄÜĮ¦ĪŖ200 m3/Š”Ź±£®Ä³³¤·½ĢåŹŅÄŚ»ī¶Æ³”µŲµÄ×ÜĆ껿ĪŖ200 m£²£¬ŹŅÄŚĒ½øß3 m£®øĆ³”µŲøŗŌšČĖ¼Ę»®¹ŗĀņ5ĢØæÕĘų¾»»ÆĘ÷ĆæĢģ»Ø·Ń30·ÖÖÓ½«ŹŅÄŚæÕĘų¾»»ÆŅ»ŠĀ£¬Čē²»æ¼ĀĒæÕĘų¶ŌĮ÷µČŅņĖŲ£¬ÖĮÉŁŅŖ¹ŗĀņAŠĶæÕĘų¾»»ÆĘ÷¶ąÉŁĢØ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Õż·½ŠĪABCDµÄ¶Ō½ĒĻßAC£¬BDĻą½»ÓŚµćO£¬½«BDĻņĮ½øö·½ĻņŃÓ³¤£¬·Ö±šÖĮµćEŗĶµćF£¬ĒŅŹ¹BE=DF£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪAECFŹĒĮāŠĪ£»
£Ø2£©ČōAC=4£¬BE=1£¬Ö±½ÓŠ“³öĮāŠĪAECFµÄ±ß³¤£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£Č«ĢåĶ¬Ń§²Ī¼ÓĮĖijĻī¾čæī»ī¶Æ£¬Ė껜³é²éĮĖ²æ·ÖĶ¬Ń§¾čæīµÄĒéæö£¬²¢Ķ³¼Ę»ęÖĘ³ÉĮĖČēĶ¼Į½·ł²»ĶźÕūµÄĢõŠĪĶ³¼ĘĶ¼ŗĶÉČŠĪĶ³¼ĘĶ¼£¬Ēėøł¾ŻĖłĢį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
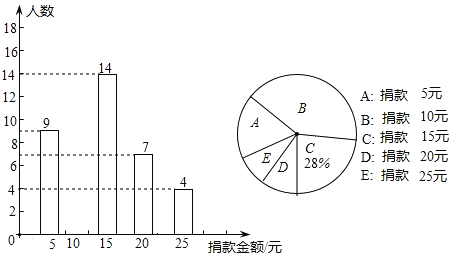
£Ø1£©±¾“Ī¹²³é²éѧɜ””””ČĖ£¬²¢½«ĢõŠĪĶ¼²¹³äĶźÕū£ŗ
£Ø2£©¾čæī½š¶īµÄÖŚŹżŹĒ””””ŌŖ£¬ÖŠĪ»ŹżŹĒ””””ŌŖ£»
£Ø3£©ČōøĆŠ£¹²ÓŠ2000Ćūѧɜ²Ī¼Ó¾čæī£¬øł¾ŻŃł±¾Ę½¾łŹż¹Ą¼ĘøĆŠ£“óŌ¼æɾčæī¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”ŃOŹĒ”÷ABCµÄĶā½ÓŌ²£¬OµćŌŚBC±ßÉĻ£¬”ĻBACµÄĘ½·ÖĻß½»”ŃOÓŚµćD£¬Į¬½ÓBD”¢CD£¬¹żµćD×÷BCµÄĘ½ŠŠĻߣ¬ÓėABµÄŃÓ³¤ĻßĻą½»ÓŚµćP£®
£Ø1£©ĒóÖ¤£ŗPDŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©ĒóÖ¤£ŗ”÷PBD”×”÷DCA£»
£Ø3£©µ±AB=6£¬AC=8Ź±£¬ĒóĻ߶ĪPBµÄ³¤£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com