
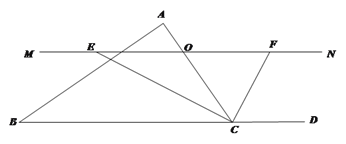
【题目】已知△ABC中,点O是边AC上的一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF.
(2)试确定点O在边AC上的位置,使四边形AECF是矩形,并加以证明.
(3)在(2)的条件下,且△ABC满足 ____________时,矩形AECF是正方形.
【答案】∠BAC=90°
【解析】分析:(1)由平行线的性质和角平分线的性质,推出∠ECB=∠CEO,∠GCF=∠CFO,∠ECB=∠ECO,∠GCF=∠OCF,通过等量代换即可推出∠CEO=∠ECO,∠CFO=∠OCF,便可确定OC=OE,OC=OF,可得OE=OF;
(2)当O点运动到AC的中点时,四边形AECF为矩形,根据矩形的判定定理(对角线相等且互相平分的四边形为矩形),结合(1)所推出的结论,即可推出OA=OC=OE=OF,求出AC=EF后,即可确定四边形AECF为矩形;
(3)当△ABC是直角三角形时,四边形AECF是正方形,根据(2)所推出的结论,由AC⊥BC,MN∥BC,确定AC⊥EF,即可推出结论.
详解:(1)∵CE是∠ACB的平分线,∴∠ACE=∠BCE.
∵MN∥BC,∴∠FEC=∠BCE,∴∠ACE=∠FEC,∴OE=OC,
同理可证OF=OC,
∴OE=OF;
(2)当点O运动到AC中点时,四边形AECF是矩形.
∵OA=OC,OE=OF,∴四边形AECF平行四边形.
∵OE=OC,∴OA=OC=OE=OF,∴AC=EF,
∴平行四边形AECF是矩形;
(3)当点O运动到AC的中点,且△ABC满足∠ACB=90°时,四边形AECF是正方形.理由如下:
∵当点O运动到AC的中点时,AO=CO.
又∵EO=FO,∴四边形AECF是平行四边形.
∵FO=CO,∴AO=CO=EO=FO,∴AO+CO=EO+FO,即AC=EF,∴四边形AECF是矩形.
∵MN∥BC,当∠ACB=90°,则∠AOF=∠COE=∠COF=∠AOE=90°,∴AC⊥EF,∴四边形AECF是正方形;
故答案为:∠ACB=90°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知 ![]() ABC的三个顶点的坐标分别为A(-1,1), B(-3,1),C(-1,4).
ABC的三个顶点的坐标分别为A(-1,1), B(-3,1),C(-1,4).
①画出△ABC关于y轴对称的△A1B1C1;
②将△ABC绕着点B顺时针旋转90°后得到△A2BC2 , 请在图中画出△A2BC2 , 并求出线段BC旋转过程中所扫过的面积(结果保留 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的(探究).
(提出问题)两个有理数a、b满足a、b同号,求![]() 的值.
的值.
(解决问题)解:由a、b同号,可知a、b有两种可能:①当a,b都正数;②当a,b都是负数.①若a、b都是正数,即a>0,b>0,有|a|=a,|b|=b,则![]() =
=![]() =1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则
=1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则![]() =
=![]() =(﹣1)+(﹣1)=﹣2,所以
=(﹣1)+(﹣1)=﹣2,所以![]() 的值为2或﹣2.
的值为2或﹣2.
(探究)请根据上面的解题思路解答下面的问题:
(1)两个有理数a、b满足a、b异号,求![]() 的值;
的值;
(2)已知|a|=3,|b|=7,且a<b,求a+b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(如图(1),在矩形ABCD中,AB=4,BC=3,点E是射线CD上的一个动点,把△BCE沿BE折叠,点C的对应点为F.
(1)若点F刚好落在线段AD的垂直平分线上时,求线段CE的长;
(2)若点F刚好落在线段AB的垂直平分线上时,求线段CE的长;
(3)当射线AF交线段CD于点G时,请直接写出CG的最大值 .


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过抛物线y= ![]() x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
(1)求抛物线的对称轴和点B的坐标;
(2)在AB上任取一点P,连结OP,作点C关于直线OP的对称点D;
①连结BD,求BD的最小值;
②当点D落在抛物线的对称轴上,且在x轴上方时,求直线PD的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的液体,并用流量、速度、密度三个概念描述车流的基本特征。其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度;密度(辆/千米)指通过道路指定断面单位长度内的车辆数,为配合大数据治堵行动,测得某路段流量q与速度v之间的部分数据如下表:
速度v(千米/小时) | … | 5 | 10 | 20 | 32 | 40 | 48 | … |
流量q(辆/小时) | … | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | … |
(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是(只需填上正确答案的序号)① ![]() ②
② ![]() ③
③ ![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足 ![]() ,请结合(1)中选取的函数关系式继续解决下列问题:
,请结合(1)中选取的函数关系式继续解决下列问题:
①市交通运行监控平台显示,当 ![]() 时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)-5.4+0.2-0.6+1.8
(2) (-26.54)+(-6.4)+18.54+6.4
(3) ![]()
(4)![]()
(5)![]()
(6) ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
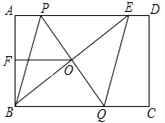
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF =4,求菱形BPEQ的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成,已知河底ED是水平的,ED=16米,AE=8米,抛物线的顶点C到ED的距离是11米,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系. 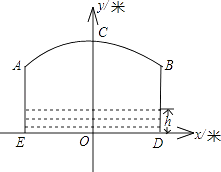
(1)根据题意,填空: ①顶点C的坐标为;
②B点的坐标为;
(2)求抛物线的解析式;
(3)已知从某时刻开始的40小时内,水面与河底ED的距离h(单位:米)随时间t(单位:时)的变化满足函数关系h=﹣ ![]() (t﹣19)2+8(0≤t≤40),且当点C到水面的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
(t﹣19)2+8(0≤t≤40),且当点C到水面的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com