
【题目】在平面直角坐标系中,已知抛物线y=x2+bx+c的对称轴为x=1,且其顶点在直线y=﹣2x﹣2上.
(1)求抛物线的顶点坐标;
(2)求抛物线的解析式;
(3)在给定的平面直角坐标系中画出这个二次函数的图象;
(4)当﹣1<x<4时,直接写出y的取值范围.

【答案】(1)(1,﹣4);(2)y=x2﹣2x﹣3;(3)详见解析;(4)﹣4≤y<5.
【解析】
(1)把x=1代入y=﹣2x﹣2即可得到结论;
(2)把抛物线的顶点坐标为(1,﹣4)代入抛物线的解析式即可得到结论.
(3)利用五点法画出图象即可;
(4)根据图象求得即可.
(1)把x=1代入y=﹣2x﹣2得,y=﹣4,
∴抛物线的顶点坐标为(1,﹣4);
(2)∵抛物线的顶点坐标为(1,﹣4);
∴抛物线的解析式为:y=(x﹣1)2﹣4,
即抛物线的解析式为:y=x2﹣2x﹣3.
(3)列表:
x |
| -1 | 0 | 1 | 2 | 3 |
|
y |
| 0 | -3 | -4 | -3 | 0 |
|
描点,连线画出图象如图:
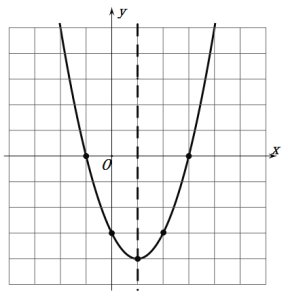
(4)当![]() 时 ,
时 ,![]() ;
;
当![]() 时 ,
时 ,![]() 有最小值-4;
有最小值-4;
当![]() 时 ,
时 ,![]() ;
;
∴当﹣1<x<4时,y的取值范围是﹣4≤y<5.


科目:初中数学 来源: 题型:
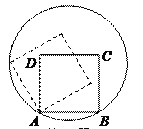
【题目】如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上, 顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为__ _.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O中,弦AB=AC,∠BAC=120°
(1)如图①,若AB=3,求⊙O的半径.
(2)如图②,点P是∠BAC所对弧上一动点,连接PB、PA、PC,试请判断PA、PB、PC之间的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机摸取一个小球然后放回,再随机摸出一个小球.
(Ⅰ)请用列表法(或画树状图法)列出所有可能的结果;
(Ⅱ)求两次取出的小球标号相同的概率;
(Ⅲ)求两次取出的小球标号的和大于6的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在生活中,有很多函数并不一定存在解析式,对于这样的函数,我们可以通过列表和图象来对它可能存在的性质进行探索,例如下面这样一个问题:
已知y是x的函数,下表是y与x的几组对应值.
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小孙同学根据学习函数的经验,利用上述表格反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
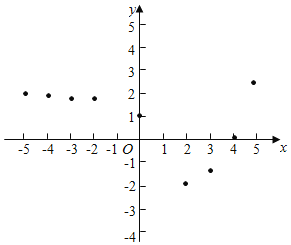
下面是小孙同学的探究过程,请补充完整;
(1)如图,在平面之间坐标系xOy中,描出了以上表中各对应值为坐标的点,根据描出的点,画出函数的图象:
(2)根据画出的函数图象回答:
①x=﹣1时,对应的函数值y的为 ;
②若函数值y>0,则x的取值范围是 ;
③写出该函数的一条性质(不能与前面已有的重复): .
查看答案和解析>>
科目:初中数学 来源: 题型:
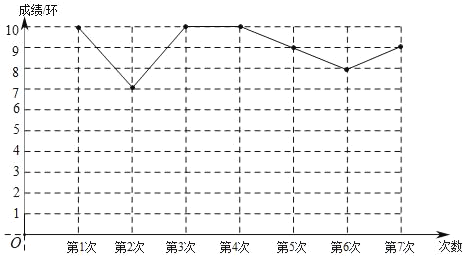
【题目】嘉淇同学利用业余时间进行射击训练,一共射击7次,经过统计,制成如图12所示的折线统计图.
(1)这组成绩的众数是 ;
(2)求这组成绩的方差;
(3)若嘉淇再射击一次(成绩为整数环),得到这8次射击成绩的中位数恰好就是原来7次成绩的中位数,求第8次的射击成绩的最大环数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题发现]
如图①,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,
上,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,则
,则![]() _____ ;
_____ ;



[拓展提高]
如图②,在等边三角形![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,直线
上,直线![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
[解决问题]
如图③,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,
,![]() .请直接写出
.请直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是弦,沿BC对折劣弧BC,交AB于D,点E、F分别是弧AB和弧BD的中点.若AD=4,AB=10,则EF=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com