
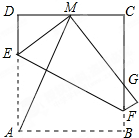
 将边长为10正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.
将边长为10正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.分析 (1)由折叠的性质得出∠AEF=∠MEF,EF⊥AM,AE=ME,得出∠EAM=∠EMA,由正方形的性质得出AB=AD=5,∠BAD=∠D=90°,证出∠MAB=∠AEF,作MG⊥AB于G,作FH⊥AD于H,得出MG=FH,由AAS证明△AMG≌△EFH,得出对应边相等即可;
(2)根据勾股定理求出AM,即可得出EF的长.
解答 (1)证明:如图: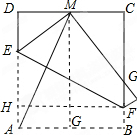
由折叠的性质得:∠AEF=∠MEF,EF⊥AM,AE=ME,
∴∠EAM=∠EMA,∠EMA+∠MEF=90°,
∵四边形ABCD是正方形,
∴AB=AD=5,∠BAD=∠D=90°,
∴∠EAM+∠MAB=90°,
∴∠MAB=∠AEF,
作MG⊥AB于G,作FH⊥AD于H,
则MG=AD,FH=AB,
∴MG=FH,
在△AMG和△EFH中,
$\left\{\begin{array}{l}{∠MAB=∠AEF}\\{∠AGM=∠EHF}\\{MG=HF}\end{array}\right.$,
∴△AMG≌△EFH(AAS),
∴AM=EF;
(2)解:在Rt△ADM中,根据勾股定理得:
AM=$\sqrt{A{D}^{2}+D{M}^{2}}$=$\sqrt{1{0}^{2}+{6}^{2}}$=2$\sqrt{34}$,
则EF=AM=2$\sqrt{34}$.
点评 本题考查了翻折变换的性质、正方形的性质、全等三角形的判定与性质、勾股定理;熟练掌握翻折变换和正方形的性质,并能进行推理论证与计算是解决问题的关键.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:解答题
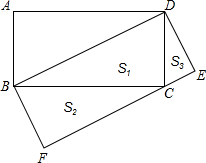 如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x+1-2x-1=1 | B. | 3x+1-2x-1=6 | C. | 3(x+1)+2(x-1)=6 | D. | 3(x+1)-2(x-1)=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com