
【题目】在学习了绝对值和有理数大小比较的知识后,老师在黑板上(如图所示)布置了作业,请完成.

【答案】(1)> ②> ③= ④=;(2)a,b异号(或ab<0);(3)-1.
【解析】
(1)①利用绝对值的性质去绝对值,进而比较大小;
②利用绝对值的性质去绝对值,进而比较大小;
③利用绝对值的性质去绝对值,进而比较大小;
④利用绝对值的性质去绝对值,进而比较大小;
(2)根据绝对值的性质结合,当a,b异号时,当a,b同号时分析得出答案;
(3)利用(2)中结论进而分析得出答案.
(1)① ∵|-2|+|6|=2+6=8,|-2+6|=4,
∴|-2|+|6|〉|-2+6|;
②∵|8|+|-4|=8+4=12,|8-4|=4,
∴|8|+|-4|>|8-4|;
③∵|-3|+|-1|=3+1=4,|-3-1|=4,
∴|-3|+|-1|=|-3-1|;
④∵|5|+|7|=5+7=12,|5+7|=12
∴|5|+|7|=|5+7|;
(2)根据(1)中的①②可得,当a、b是异号时,|a|+|b|>|a+b|;
(3)∵|x|+|10|>|x+10|
∴x和10是异号
∴x是负数
∴x的最大整数值为-1.`


科目:初中数学 来源: 题型:
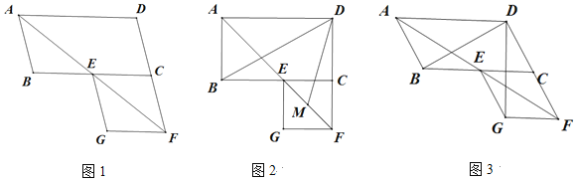
【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级全体320名学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,用抽签方式得到其中32名学生的两次考试考分等级,所绘制的统计图如图所示.试结合图示信息回答下列问题:

(1)这32名学生培训前考分的中位数所在的等级是 ,培训后考分的中位数所在的等级是 .
(2)这32名学生经过培训,考分等级“不合格” 的百分比由 下降到 .
(3)估计该校整个八年级中,培训后考分等级为“合格”与“优秀”的学生共有 名.
(4)你认为上述估计合理吗:理由是什么?
答: ,理由: .
查看答案和解析>>
科目:初中数学 来源: 题型:
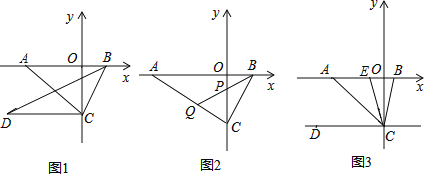
【题目】如图1,在平面直角坐标系中,点A为x轴负半轴上一点,点B为x轴正半轴上一点,![]() ,
,![]() ,其中a、b满足关系式:
,其中a、b满足关系式:![]() .
.
![]() ______,
______,![]() ______,
______,![]() 的面积为______;
的面积为______;
![]() 如图2,石
如图2,石![]() 于点C,点P是线段OC上一点,连接BP,延长BP交AC于点
于点C,点P是线段OC上一点,连接BP,延长BP交AC于点![]() 当
当![]() 时,求证:BP平分
时,求证:BP平分![]() ;
;![]() 提示:三角形三个内角和等于
提示:三角形三个内角和等于![]()
![]() 如图3,若
如图3,若![]() ,点E是点A与点B之间上一点连接CE,且CB平分
,点E是点A与点B之间上一点连接CE,且CB平分![]() 问
问![]() 与
与![]() 有什么数量关系?请写出它们之间的数量关系并请说明理由.
有什么数量关系?请写出它们之间的数量关系并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
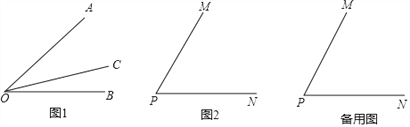
【题目】【探索新知】:如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线 这个角的“巧分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ= ;(用含α的代数式表示出所有可能的结果)
【深入研究】:如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.
(3)当t为何值时,射线PM是∠QPN的“巧分线”;
(4)若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是∠MPN的“巧分线”时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(1)问题解决:受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(2)问题拓展:如图3,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).


图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究1:如图l,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90![]() +
+![]() ∠A,理由如下:
∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴∠1=![]() ∠ABC, ∠2=
∠ABC, ∠2=![]() ∠ACB
∠ACB
∴∠l+∠2=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180
(180![]() -∠A)= 90
-∠A)= 90![]() -
-![]() ∠A
∠A
∴∠BOC=180![]() -(∠1+∠2) =180
-(∠1+∠2) =180![]() -(90
-(90![]() -
-![]() ∠A)=90
∠A)=90![]() +
+![]() ∠A
∠A
(1)探究2;如图2中,O是![]() ∠ABC与外角
∠ABC与外角![]() ∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
(2)探究3:如图3中, O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(直接写出结论)
(3)拓展:如图4,在四边形ABCD中,O是∠ABC与∠DCB的平分线BO和CO的交点,则∠BOC与∠A+∠D有怎样的关系?(直接写出结论)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图∠1=∠2,CF⊥AB,DE⊥AB,求证:FG∥BC.
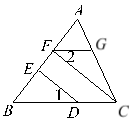
证明:∵CF⊥AB,DE⊥AB (已知)
∴∠BED=90°,∠BFC=90°( )
∴∠BED=∠BFC ( )
∴ED∥FC ( )
∴∠1=∠BCF ( )
∵∠2=∠1 ( 已知 )
∴∠2=∠BCF ( )
∴FG∥BC ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com